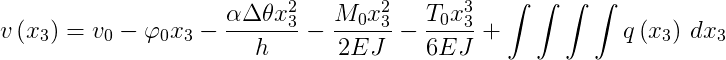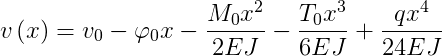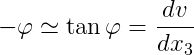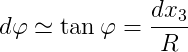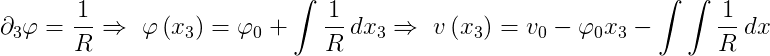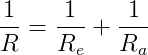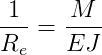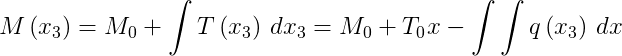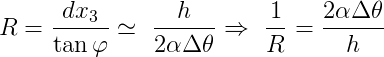Linea elastica flessionale

Da TecnoLogica.

Descrizione

Per flessionale si intende la linea elastica che esprime gli spostamenti dei punti di un'asta perpendicolari all'asse. Gli spostamenti collineari a detto asse sono invece espressi dalla linea elastica estensionale.
Nella meccanica, è importante distinguere due casi. Il primo, più semplice, considera che spostamenti e rotazioni sono infinitesime: in tal modo possono introdursi notevoli semplificazioni nei calcoli; inoltre, è possibile separare gli effetti di taglio e momento flettente (flessionali) da quelli di sforzo normale (estensionale) e momento torcente (che non produce linea elastica). Fortunatamente, molti materiali da costruzione hanno un comportamento che può essere bene espresso in questo modo.
Il secondo, molto più complesso, considera spostamenti e rotazioni finite, per cui anche taglio e flessione possono avere riflessi nella linea elastica estensionale; inoltre, il problema differenziale diviene notevolmente complicato, e le equazioni che ne derivano sono di difficile soluzione.

Spostamenti infinitesimi

Nella pratica costruttiva, i materiali e gli elementi tecnici che caratterizzano le strutture permettono di introdurre delle semplificazioni significative, che consentono di risolvere il problema della ricerca della linea elastica con maggiore facilità. Queste semplificazioni sono:

• spostamenti e rotazioni infinitesimi;
• lunghezza dell'asta preponderante rispetto alle dimensioni della sezione trasversale;
• bordo scarico (sostituire le caratteristiche di sollecitazione al carico vero e proprio, come avviene in un solido di de Saint Venant);
• deformazione dovuta al momento flettente preponderante rispetto al taglio.

La linea elastica, nella sua formulazione generale in presenza di curvature elastiche ed anelastiche ed in tema di spostamenti infinitesimi, assume la forma:

,

dove sono i valori che assumono nell'origine l'abbassamento, la rotazione, il momento flettente (di solito, la caratteristica di sollecitazione M₁) e il taglio (di solito, caratteristica di sollecitazione T₂); è la curvatura anelastica dovuta ad una distorsione termica a farfalla positiva, e è la legge di variazione del carico.
Nel caso, molto frequente, di assenza di curvature anelastiche e di carichi costanti, la linea elastica si riduce a:

.

Per determinare la linea elastica flessionale su un'asta occorre prima di tutto suddividerla in tronchi, cioè in tratti in cui si riscontrano condizioni di continuità, sia statiche che cinematiche.
In altre parole, punti in cui sono presenti discontinuità statiche e cinematiche suddividono la linea elastica di un'asta continua in una serie di tratti, per ognuno dei quali deve essere ricercata una diversa equazione della linea elastica.
Le discontinuità che interrompono un'asta rendendo necessaria la scrittura di più equazioni sono:

• la presenza di angoli nell'asse dell'asta;
• vincoli, sia a terra che interni;
• carichi statici concentrati (forze e momenti)
• discontinuità nella legge di variazione di carichi distribuiti;
• distorsioni concentrate (di scorrimento e di rotazione).

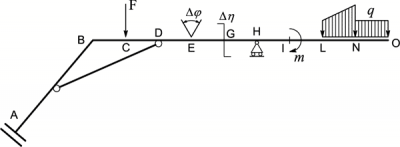
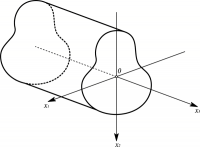
La struttura raffigurata a lato, ad esempio, nel tratto BO deve essere divisa in nove tronchi a causa delle discontinuità presenti.

Dimostrazione

Se gli spostamenti sono infinitesimi, l'equazione della linea elastica flessionale può essere dimostrata grazie all'impiego delle relazioni esistenti tra le entità della cinematica e della statica che caratterizzano un solido di de Saint Venant. Nel ricercare queste equazioni, assume una grande importanza il sistema di riferimento adottato, perché da esso dipende la positività o la negatività dei termini presenti nella linea elastica finale.
Si utilizzeranno nella dimostrazione:

• legami cinematici: due relazioni differenziali che legano lo spostamento alla rotazione, e la rotazione alla curvatura;
• legami statici: due relazioni differenziali che legano il momento flettente al taglio, ed il taglio al carico statico sull'asta;
• legame costitutivo: una relazione che lega la curvatura elastica al momento flettente.

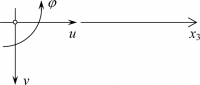
Per dimostrare le prime due relazioni, che correlano spostamento, rotazione e curvatura, è necessario specificare che la terna di assi adottata è di tipo destrogiro, cioè opposta a quelle che comunemente vengono impiegate nella fisica. In particolare, facendo coincidere l'asse degli spostamenti orizzontali u con l'asse x₃ dell'asta^[1], e considerando positivo il verso antiorario per le rotazioni φ, l'asse degli spostamenti verticali v ha verso positivo in basso. Questo perché in generale quando le aste orizzontali (travi) vengono inflesse, i loro punti si spostano verso il basso, ed è più comodo indicare l'abbassamento come spostamento positivo.

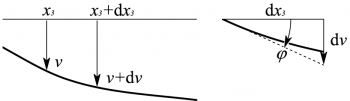
La prima relazione lega l'abbassamento v con la rotazione φ. Preso sull'asse dell'asta indeformata un punto ad una ascissa x₃, con abbassamento infinitesimo positivo v, un secondo punto infinitesimamente prossimo, di ascissa x₃ + dx₃, avrà un abbassamento anch'esso infinitesimo e positivo v+dv. La distanza tra i due punti sarà quindi dx₃, mentre la differenza tra gli abbassamenti sarà dv.
Trovandosi il secondo punto in un intorno del primo, è possibile confondere in quell'intervallo la linea elastica con la retta tangente, che sarà ruotata rispetto all'asse indeformato di un angolo infinitesimo e orario (quindi negativo) -φ; è possibile quindi scrivere la relazione:

,

ovvero:

.

Ciò significa, tra l'altro, che ad una rotazione positiva (antioraria) corrisponde uno spostamento negativo (verso l'alto) e, al contrario, ad un abbassamento corrisponde una rotazione negativa (oraria).

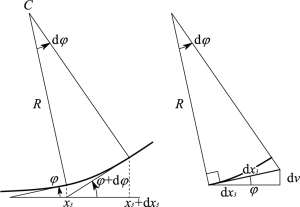
La seconda equazione può essere trovata assegnando una deformazione con rotazione positiva (antioraria) sulla quale viene individuato un punto di ascissa x₃ ed uno ad esso successivo, in un intorno infinitesimo, di ascissa x₃ + dx₃. Siano φ e φ + dφ le rispettive rotazioni, e si traccino le tangenti a questi due punti; disegnate quindi le perpendicolari alle tangenti passanti per i punti sulla deformata, queste individueranno un punto C che rappresenta il centro di curvatura della linea elastica riferito al primo dei due punti scelti. La sua distanza R da questo punto è invece detta raggio di curvatura, mentre il suo inverso 1/R si dice semplicemente curvatura. Seguendo semplici considerazioni aritmetiche, è immediato verificare come l'angolo che si forma nel centro C è proprio pari all'incremento dφ. Costruendo un triangolo rettangolo avente un vertice in C e cateto maggiore R, è possibile determinare la relazione che intercorre tra dφ ed R se si conosce la lunghezza del secondo cateto. Tale valore può essere determinato facilmente perché, visto che spostamenti e rotazioni della linea elastica sono infinitesimi, può essere approssimato a dx₃. È quindi possibile calcolare il valore di dφ come:

,

e quindi:

.

La curvatura di una trave a sua volta può essere espressa come la somma di una curvatura elastica dovuta alla presenza del momento flettente, e di una curvatura anelastica dovuta alla eventuale presenza di distorsioni termiche a farfalla; in termini formali si può scrivere quindi:

.

La curvatura elastica, come dimostrato nella flessione, è pari a:

,

dove E è il modulo di Young e J è l'inerzia relativa all'asse di sollecitazione^[2]. La relazione sopra riportata è generalmente nota come legame costitutivo.

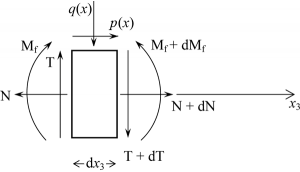
La legge di variazione del momento può essere facilmente ricavata imponendo, su un concio infinitesimo, gli equilibri alla traslazione verticale ed alla rotazione. Dal primo infatti si ottiene:

da cui si ottiene che:

.

Imponendo poi l'equilibrio alla rotazione nel baricentro della sezione posta a destra (dove agiscono le sollecitazioni incrementate), si ottiene:

,

dove , e quindi:

.

Inserendo quindi questa espressione nel legame costitutivo, si ottiene che:

.

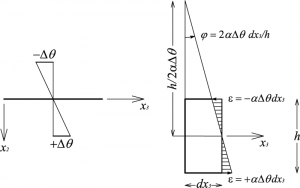
Resta quindi da stabilire il valore di 1/R_a dovuto ad una distorsione termica a farfalla eventualmente presente sull'asta. Assegnata una distorsione positiva - cioè che tende le fibre inferiori dell'asta, detto α il coefficiente di dilatazione termica del materiale, e ±Δθ lo scarto termico presente sui bordi superiore e inferiore della sezione, le deformazioni massima e minima su un concio infinitesimo saranno pari a:

.

La rotazione (infinitesima) relativa tra le due facce sarà invece:

,

dove h è l'altezza della sezione. A questo punto il raggio di curvatura può essere facilmente determinato come:

.

Inserendo questo valore nella linea elastica ed integrando due volte, si ottiene la relazione:

,

che rappresenta l'espressione generale cercata.

Voci correlate

• Distorsione termica a farfalla
• Flessione
• Linea elastica
• Teoria della trave

Note

1. ↑
   
   Gli assi dell'asta sono generalmente disposti nel seguente modo: su ogni sezione si individua il baricentro, in cui si pone il centro del sistema di riferimento; perpendicolarmente alla sezione, ed uscente da essa, si pone l'asse x₃.
   Gli assi x₁ e x₂ sono invece principali di inerzia, con x₂ concorde, quando possibile, con la direzione della gravità (cioè, in parole povere, direzionato verso il basso), e x₁ di verso tale da ottenere una terna levogira.
   Se la flessione è sollecitata dal momento M₁, allora x₂ = v e x₃ = - φ.
2. ↑ Se sulla sezione agisce M₁, allora 1/R_e = M₁/EJ₁; se invece è presente M₂, allora 1/R_e = M₂/EJ₂.

La consultazione di TecnoLogica è preordinata alla lettura delle avvertenze Ogni contributore è responsabile dei propri inserimenti. Il progetto è opera di Luca Buoninconti © 2011-2024.