Linea elastica estensionale

Da TecnoLogica.

Descrizione

Per estensionale si intende la linea elastica che esprime gli spostamenti dei punti di un'asta collineari all'asse. Gli spostamenti perpendicolari a detto asse sono invece espressi dalla linea elastica flessionale.
Nella meccanica, è importante distinguere due casi. Il primo, più semplice, considera che spostamenti e rotazioni sono infinitesime: in tal modo possono introdursi notevoli semplificazioni nei calcoli; inoltre, è possibile separare gli effetti di taglio e momento flettente (flessionali) da quelli di sforzo normale (estensionale) e momento torcente (che non produce linea elastica). Fortunatamente, molti materiali da costruzione hanno un comportamento che può essere bene espresso in questo modo.
Il secondo, molto più complesso, considera spostamenti e rotazioni finite, per cui anche taglio e flessione possono avere riflessi nella linea elastica estensionale; inoltre, il problema differenziale diviene notevolmente complicato, e le equazioni che ne derivano sono di difficile soluzione.

Spostamenti infinitesimi

Nella pratica costruttiva, i materiali e gli elementi tecnici che caratterizzano le strutture permettono di introdurre delle semplificazioni significative, che consentono di risolvere il problema della ricerca della linea elastica con maggiore facilità. Queste semplificazioni sono:

spostamenti e rotazioni infinitesimi;
lunghezza dell'asta preponderante rispetto alle dimensioni della sezione trasversale;
bordo scarico (sostituire le caratteristiche di sollecitazione al carico vero e proprio, come avviene in un solido di de Saint Venant);
deformazione dovuta al momento flettente ed al taglio ininfluente sulla linea estensionale.

La linea elastica, nella sua formulazione generale in presenza di allungamenti elastici ed anelastici ed in tema di spostamenti infinitesimi, assume la forma:

$LaTeX: u \left( x \right) = u_0 + \frac{N_0 x}{EA} + \alpha \Delta \vartheta x - \frac{1}{EA} \int \int p \left( x \right) \, \mathbb{d}x$ ,

dove $LaTeX: u_0$ e $LaTeX: N_0$ sono i valori che assumono nell'origine l'allungamento e lo sforzo normale; $LaTeX: \alpha \Delta$ è la deformazione estensionale anelastica dovuta ad una distorsione termica distribuita positiva e uniforme^[1], e $LaTeX: p \left( x \right)$ è la legge di variazione del carico distribuito lungo l'asse.
Nel caso, molto frequente, di assenza di deformazioni anelastiche e di carichi costanti, la linea elastica si riduce a:

$LaTeX: u \left( x \right) = u_0 + \frac{N_0 x}{EA} - \frac{p x^2}{2EA}$ .

Per determinare la linea elastica estensionale su un'asta occorre prima di tutto suddividerla in tronchi, cioè in tratti in cui si riscontrano condizioni di continuità, sia statiche che cinematiche.
In altre parole, punti in cui sono presenti discontinuità statiche e cinematiche suddividono la linea elastica di un'asta continua in una serie di tratti, per ognuno dei quali deve essere ricercata una diversa equazione della linea elastica.
Le discontinuità che interrompono un'asta rendendo necessaria la scrittura di più equazioni sono:

la presenza di angoli nell'asse dell'asta;
vincoli, sia a terra che interni, con reazioni lungo l'asse della trave;
carichi statici concentrati (forze e momenti) diretti lungo l'asse della trave;
discontinuità nella legge di variazione di carichi assiali distribuiti;
distorsioni concentrate (di tipo assiale).

Dimostrazione

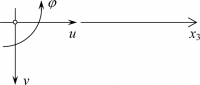
Se gli spostamenti sono infinitesimi, l'equazione della linea elastica estensionale può essere dimostrata grazie all'impiego delle relazioni esistenti tra le entità della cinematica e della statica che caratterizzano un solido di de Saint Venant. Il sistema di riferimento adottato è rappresentato a lato, dove l'asse $LaTeX: u$ è collineare ed equiverso all'asse $LaTeX: x_3$ .
Si utilizzeranno nella dimostrazione:

legame cinematico: una relazione differenziale che lega lo spostamento alla deformazione;
legame statico: una relazione differenziale che lega losforzo normale al carico statico assiale;
legame costitutivo: una relazione che lega la deformazione elastica allo sforzo normale.

La prima relazione è derivata direttamente dall'analisi della deformazione; ricordando che:

$LaTeX: \epsilon_{ij} = \frac{1}{2} \left( u_{j,i} + u_{i,j} \right)$ ,

si ottiene facilmente che:

$LaTeX: \epsilon_{33} = u_{3,3}$ .

Nel sistema di riferimento adottato, risulta che $LaTeX: u$ è proprio lo spostamento $LaTeX: u_3$ nella direzione $LaTeX: x_3$ , da cui si ottiene che:

$LaTeX: u \left( x_3 \right) = u_0 + \int \epsilon_{33} \left( x_3 \right) \,\mathbb{d}x_3$ .

La deformazione $LaTeX: \epsilon_{33}$ è in generale originata da un'aliquota anelastica e da una elastica. In termini formali può scriversi:

$LaTeX: \epsilon_{33} = \epsilon_{33,e} + \epsilon_{33,a}$ .

La deformazione elastica è pari a:

$LaTeX: \epsilon_{33} = \frac{\sigma_{33}}{E}$ ,

dove $LaTeX: E$ rappresenta il modulo di Young. Ricordando che nella teoria della trave:

$LaTeX: N \left( x_3 \right) = \frac{\sigma_{33}}{A}$ ,

dove $LaTeX: A$ è l'area della sezione, si ottiene:

$LaTeX: \epsilon_{33} = \frac{N}{EA}$ .

Tale è il legame costitutivo che consente di relazionare la deformazione (cinematica) con la tensione (statica) nell'asta.

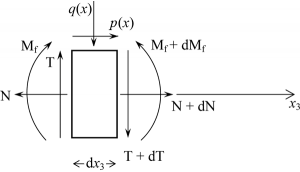
La relazione che permette invece di esprimere la legge di variazione dello sforzo normale si ricava imponendo, sul concio infinitesimo, si ottiene imponendo l'equilibrio alla traslazione orizzontale, ed in particolare:

$LaTeX: R_3 = 0 \Rightarrow \ - N + N + dN + p\left( x_3 \right)dx_3 = 0 \Rightarrow \ \frac{dN}{dx_3} = \partial_3 N = -p\left( x_3 \right)$

da cui si ottiene che:

$LaTeX: N \left( x_3 \right) = N_0 - \int p \left( x_3 \right) \,\mathbb{d}x_3$ .

Inserendo quindi questa espressione nel legame costitutivo, si ottiene che:

$LaTeX: u \left( x_3 \right) = u_0 + \frac{N x_3}{EA} - \int \int p \left( x_3 \right) \,\mathbb{d}x_3 + \int \epsilon_{33,a} \left( x_3 \right) \,\mathbb{d}x_3$ .

Resta da stabilire il valore di $LaTeX: \epsilon_{33,a}$ . Gli allungamenti (o accorciamenti) anelastici sono originati da distorsioni termiche distribuite lungo la lunghezza dell'asta; di solito tale carico geometrico è uniforme, e può essere conosciuto quando sono noti il coefficiente di dilatazione termica del materiale e la variazione di temperatura $LaTeX: \Delta \vartheta$ . In tal caso si ottiene che:

$LaTeX: \epsilon_{33,a} = \Alpha \Delta \vartheta$ ;

inserendo questo valore nella linea elastica si ottiene l'espressione:

$LaTeX: u \left( x \right) = u_0 + \frac{N_0 x}{EA} + \alpha \Delta \vartheta x - \frac{1}{EA} \int \int p \left( x \right) \, \mathbb{d}x$ ,

che rappresenta la relazione generale cercata.

Voci correlate

Note

↑ Sono infatti rari i casi in cui la distorsione termica non è uniforme.

La consultazione di TecnoLogica è preordinata alla lettura delle avvertenze

[0] Sono infatti rari i casi in cui la distorsione termica non è uniforme.

[1]

Linea elastica estensionale

Da TecnoLogica.

Descrizione

Spostamenti infinitesimi

Dimostrazione

Voci correlate

Note

Visite

Strumenti personali

Navigazione

Ricerca

Strumenti