Spazio vettoriale

Da TecnoLogica.

(Differenze fra le revisioni)

Versione delle 08:51, 4 apr 2017

Questa pagina contiene una o più parti ancora in corso di compilazione. Queste sono segnalate dalle diciture da compilare e/o da completare.

I contributori si impegnano a rendere disponibile e completo il lemma nel più breve tempo possibile.

Struttura algebrica costituita da un campo, il cui insieme di sostegno viene detto insieme degli scalari, un insieme di elementi detti vettori, e due operazioni dette prodotto per uno scalare e somma vettoriale.

Descrizione

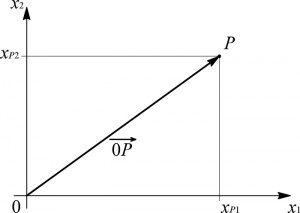
Sia dato uno spazio piano nel quale 0 x₁ x₂ è un sistema di riferimento cartesiano, che per semplicità considereremo ortogonale: come è noto, ad ogni punto P corrisponde una ed una sola coppia di valori (x_P1, x_P2) e, viceversa, ad ogni coppia di numeri reali (x_P1, x_P2) corrisponde uno ed un solo punto P del piano.
In termini formali, il sistema di assi permette di costruire una relazione biunivoca tra i punti del piano e le coppie di numeri reali, e cioè:

$LaTeX: \mathcal {f} : \mathbb{S}^2 \leftrightarrow \mathbb{R}^2$ ,

dove per $LaTeX: \mathbb{S}^2$ si intende l'insieme dei punti del piano e per $LaTeX: \mathbb{R}^2$ il prodotto cartesiano dell'insieme dei numeri reali per sé stesso.
Allo stesso modo, ad ogni punto P è possibile far corrispondere un vettore applicato nell'origine 0, detto $LaTeX: \overrightarrow{0P}$ , e cioè un segmento orientato da 0 a P rappresentabile come una freccia avente punta in P.
È evidente che è possibile costruire una relazione biunivoca tra tutti i punti e tutti i vettori del piano perché ad ogni punto corrisponderà uno ed un solo vettore, e viceversa. In termini formali, sarà:

$LaTeX: \mathcal {g} : \mathbb{S}^2 \leftrightarrow \mathcal{V}_2$ ,

dove $LaTeX: \mathcal{V}_2$ rappresenta l'insieme di tutti i vettori piani.
Ne consegue quindi che, stabilito un sistema di riferimento, deve sussistere una relazione biunivoca tra tutte coppie di numeri reali e tutti i vettori piani applicati all'origine degli assi, cioè:

$LaTeX: \mathcal {h} : \mathbb{R}^2 \leftrightarrow \mathcal{V}_2$ .

Per stabilire tale legame, occorre introdurre tre concetti fondamentali per la definizione dello spazio vettoriale, ed in particolare:

introdurre la base vettoriale;
definire l'operazione di prodotto per uno scalare;
precisare l'operazione di somma vettoriale.

La base vettoriale è l'equivalente del sistema di assi cartesiani nella geometria analitica: si tratta di stabilire nel piano $LaTeX: \mathbb{S}^2$ una coppia di vettori (per comodità ortogonali tra loro) applicati in un punto origine 0 ed avente lunghezza unitaria, e che per tale ultimo motivo sono detti versori.
In generale quindi un versore è un vettore unitario, e si indica genericamente con $LaTeX: \hat{\mathbf{e}}_n$ ; una coppia di versori non paralleli aventi origine in comune si dice base vettoriale; infine, una coppia di versori aventi origine in comune e tra loro perpendicolari prende il nome di base ortonormale.
Le basi ortonormali, collineari agli assi x₁ e x₂ e con i quali condividono la medesima origine 0, vengono indicati come $LaTeX: \hat{\mathbf{e}}_1$ e $LaTeX: \hat{\mathbf{e}}_2$ .

Il prodotto per uno scalare è un'operazione tra un numero reale $LaTeX: r$ ed un vettore $LaTeX: \bar{\mathbf{v}}$ ; si indica con il simbolo $LaTeX: \cdot$ (esempio: $LaTeX: r \cdot \bar{\mathbf{v}}$ ) o omettendo il simbolo (esempio: $LaTeX: r \bar{\mathbf{v}}$ ), e si legge "per" (esempio: $LaTeX: r \cdot \bar{\mathbf{v}}$ si pronuncia erre per vi). Il risultato è un nuovo vettore $LaTeX: \bar{\mathbf{w}}$ avente:

la stessa direzione di $LaTeX: \bar{\mathbf{v}}$ ;
lo stesso verso di $LaTeX: \bar{\mathbf{v}}$ se $LaTeX: r$ è positivo, e verso opposto se $LaTeX: r$ è negativo;
lunghezza pari a $LaTeX: r$ volte la lunghezza di $LaTeX: \bar{\mathbf{v}}$ o per essere precisi, indicando con $LaTeX: \left | \bar{\mathbf{v}} \right |$ il modulo di $LaTeX: \bar{\mathbf{v}}$ (modulo equivale a lunghezza) e con $LaTeX: \left | \bar{\mathbf{w}} \right |$ il modulo di $LaTeX: \bar{\mathbf{w}}$ , allora $LaTeX: \left | \bar{\mathbf{w}} \right |= r \left | \bar{\mathbf{v}} \right |$ .

Assegnando quindi generica direzione $LaTeX: n$ ed un suo versore $LaTeX: \hat{\mathbf{e}}_n$ , è possibile ottenere tutti i vettori giacenti su quella direzione moltiplicando di volta in volta il versore per tutti i numeri reali; in altre parole, il generico vettore $LaTeX: \bar{\mathbf{v}}_n$ giacente sulla direzione $LaTeX: n$ avente lunghezza $LaTeX: v$ può essere ottenuto attraverso il prodotto per uno scalare $LaTeX: v \cdot \hat{\mathbf{e}}_n$ se ha lo spesso verso di $LaTeX: \hat{\mathbf{e}}_n$ , e come $LaTeX: - v \cdot \hat{\mathbf{e}}_n$ se ha verso opposto.
I numeri reali prendono il nome di scalari perché attraverso il prodotto per uno scalare sono in grado di aumentare e/o ridurre la lunghezza di un vettore, e quindi funzionano come fattore di scala. L'insieme dei numeri reali $LaTeX: \mathbb{R}$ prende quindi il nome di insieme degli scalari.

La somma vettoriale è un'operazione tra due vettori $LaTeX: \bar{\mathbf{a}}$ e $LaTeX: \bar{\mathbf{b}}$ ; si indica con il simbolo $LaTeX: +$ (esempio: $LaTeX: \bar{\mathbf{a}} + \bar{\mathbf{b}}$ ) e si legge "più" (esempio: $LaTeX: \bar{\mathbf{a}} + \bar{\mathbf{b}}$ si pronuncia a più bi). Il risultato è un nuovo vettore determinato con la nota regola del parallelogramma: traslati i vettori addendi $LaTeX: \bar{\mathbf{a}}$ e $LaTeX: \bar{\mathbf{b}}$ nel medesimo punto di applicazione (a volte per comodità si può utilizzare l'origine degli assi), si costruisce un parallelogrammo avente per lati proprio i vettori "addendi" (gli altri due si determinano per parallelismo); il vettore che giace sulla diagonale che parte dal punto di applicazione è il vettore somma, che viene detto vettore risultante, o più brevemente la risultante della somma vettoriale.

(Da completare)

Voci correlate

La consultazione di TecnoLogica è preordinata alla lettura delle avvertenze

@@ Riga 35: / Riga 35: @@
 Assegnando quindi generica direzione <math>n</math> ed un suo versore <math> \hat{\mathbf{e}}_n </math>, è possibile ottenere tutti i vettori giacenti su quella direzione moltiplicando di volta in volta il versore per tutti i numeri reali; in altre parole, il generico vettore <math> \bar{\mathbf{v}}_n</math> giacente sulla direzione <math>n</math> avente lunghezza <math>v</math> può essere ottenuto attraverso il prodotto per uno scalare <math>v \cdot \hat{\mathbf{e}}_n</math> se ha lo spesso verso di <math> \hat{\mathbf{e}}_n </math>, e come <math>- v \cdot \hat{\mathbf{e}}_n</math> se ha verso opposto.<br/>
 I numeri reali prendono il nome di '''scalari''' perché attraverso il prodotto per uno scalare sono in grado di aumentare e/o ridurre la lunghezza di un vettore, e quindi funzionano come fattore di scala. L'insieme dei numeri reali <math> \mathbb{R} </math> prende quindi il nome di '''insieme degli scalari'''.
+La '''somma vettoriale''' è un'operazione tra due vettori <math> \bar{\mathbf{a}} </math> e <math> \bar{\mathbf{b}} </math>; si indica con il simbolo <math> + </math> (esempio: <math> \bar{\mathbf{a}} + \bar{\mathbf{b}} </math>) e si legge "''più''" (esempio: <math> \bar{\mathbf{a}} + \bar{\mathbf{b}} </math> si pronuncia ''a più bi''). Il risultato è un nuovo vettore determinato con la nota '''regola del parallelogramma''': traslati i vettori addendi <math> \bar{\mathbf{a}} </math> e <math> \bar{\mathbf{b}} </math> nel medesimo punto di applicazione (a volte per comodità si può utilizzare l'origine degli assi), si costruisce un parallelogrammo avente per lati proprio i vettori "addendi" (gli altri due si determinano per parallelismo); il vettore che giace sulla diagonale che parte dal punto di applicazione è il vettore somma, che viene detto '''vettore risultante''', o più brevemente la '''risultante''' della somma vettoriale.
 (''Da completare'')
@@ Riga 41: / Riga 43: @@
 *[[Struttura algebrica]]
 *[[Vettore]]
-*[[Tensore]]
+*[[Tensore]]e
 {{Footer}}
 [[Category:Matematica]]

Spazio vettoriale

Da TecnoLogica.

Versione delle 08:51, 4 apr 2017

Descrizione

Voci correlate

Visite

Strumenti personali

Navigazione

Ricerca

Strumenti