Spazio vettoriale

Da TecnoLogica.

Consulta TecnoLogica solo dopo aver letto le avvertenze!

Struttura algebrica costituita da un campo, il cui insieme di sostegno viene detto insieme degli scalari, un insieme di elementi detti vettori, e due operazioni dette prodotto per uno scalare e somma vettoriale.

Descrizione

Lo spazio vettoriale è una struttura algebrica, cioè un insieme formato da:

un sostegno, cioè un insieme di elementi con i quali, attraverso due operazioni ed una base vettoriale, vengono generati i vettori;
una base vettoriale, cioè un insieme di vettori linearmente indipendenti assunti come elementi di partenza per ottenere tutti gli altri vettori;
un’operazione detta prodotto per uno scalare, attraverso la quale è possibile modificare l’intensità di un vettore;
un’operazione detta somma vettoriale, con la quale si può ottenere un vettore come composizione (somma) di altri due.

Scegliendo opportunamente il sostegno dello spazio vettoriale (il campo ℝ dei numeri reali) e le operazioni di prodotto e somma, è possibile creare una corrispondenza biunivoca tra uno spazio ad n dimensioni 𝕊 ⁿ e uno spazio vettoriale n-dimensionale .

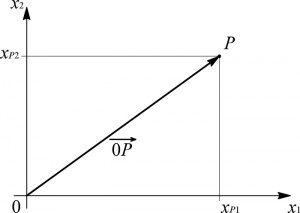
Sia dato uno spazio piano nel quale 0 x₁ x₂ è un sistema di riferimento cartesiano, che per semplicità considereremo ortogonale: come è noto, ad ogni punto P corrisponde una ed una sola coppia di valori (x_P1, x_P2) e, viceversa, ad ogni coppia di numeri reali (x_P1, x_P2) corrisponde uno ed un solo punto P del piano.
In termini formali, il sistema di assi permette di costruire una relazione biunivoca tra i punti del piano e le coppie di numeri reali, e cioè:

,

dove per 𝕊 ² si intende l'insieme dei punti del piano e per ℝ ² il prodotto cartesiano dell'insieme dei numeri reali per sé stesso.
Allo stesso modo, ad ogni punto P è possibile far corrispondere un vettore applicato nell'origine 0, detto , e cioè un segmento orientato da 0 a P rappresentabile come una freccia avente punta in P.
È evidente che è possibile costruire una relazione biunivoca tra tutti i punti e tutti i vettori del piano perché ad ogni punto corrisponderà uno ed un solo vettore, e viceversa. In termini formali, sarà:

,

dove rappresenta l'insieme di tutti i vettori piani.
Ne consegue quindi che, stabilito un sistema di riferimento, deve sussistere una relazione biunivoca tra tutte coppie di numeri reali e tutti i vettori piani applicati all'origine degli assi, cioè:

.

Per stabilire tale legame, occorre introdurre tre concetti fondamentali per la definizione dello spazio vettoriale, ed in particolare:

introdurre la base vettoriale;
definire l'operazione di prodotto per uno scalare;
precisare l'operazione di somma vettoriale.

Base vettoriale

La base vettoriale è l'equivalente del sistema di assi cartesiani nella geometria analitica: si tratta di stabilire nel piano 𝕊 ² una coppia di vettori (per comodità ortogonali tra loro) applicati in un punto origine 0 ed avente lunghezza unitaria, e che per tale ultimo motivo sono detti versori.
In generale quindi un versore è un vettore unitario, e si indica genericamente con ; una coppia di versori non paralleli aventi origine in comune si dice base vettoriale; infine, una coppia di versori aventi origine in comune e tra loro perpendicolari prende il nome di base ortonormale.
Le basi ortonormali, collineari agli assi x₁ e x₂ e con i quali condividono la medesima origine 0, vengono indicati come e .

Prodotto per uno scalare

Il prodotto per uno scalare è un'operazione tra un numero reale r ed un vettore ; si indica con il simbolo • (esempio: r • ) o omettendo il simbolo (esempio: r ), e si legge "per" (esempio: erre per vi). Il risultato è un nuovo vettore avente:

la stessa direzione di ;
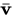lo stesso verso di 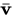se r è positivo, e verso opposto se r è negativo;
lunghezza pari a r volte la lunghezza di 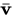o per essere precisi, indicando con | 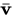| il modulo di 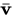(modulo equivale a lunghezza) e con | 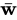| il modulo di 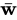, allora | 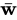| = r | |.

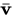Assegnando quindi generica direzione n ed un suo versore , è possibile ottenere tutti i vettori giacenti su quella direzione moltiplicando di volta in volta il versore per tutti i numeri reali; in altre parole, il generico vettore _n giacente sulla direzione n avente lunghezza v può essere ottenuto attraverso il prodotto per uno scalare v • se ha lo stesso verso di , e come –v • se ha verso opposto.
I numeri reali prendono il nome di scalari perché attraverso il prodotto per uno scalare sono in grado di aumentare e/o ridurre la lunghezza di un vettore, e quindi funzionano come fattore di scala. L'insieme dei numeri reali ℝ prende quindi il nome di insieme degli scalari.

Somma vettoriale

La somma vettoriale è un'operazione tra due vettori e ; si indica con il simbolo + (esempio: + ) e si legge "più" (esempio: + si pronuncia a più bi). Il risultato è un nuovo vettore determinato con la nota regola del parallelogramma: traslati i vettori addendi, ad esempio: e , nel medesimo punto di applicazione (a volte per comodità si può utilizzare l'origine degli assi), si costruisce un parallelogrammo avente per lati proprio i vettori "addendi" (gli altri due si determinano per parallelismo); il vettore che giace sulla diagonale che parte dal punto di applicazione è il vettore somma, che viene detto vettore risultante, o più brevemente la risultante della somma vettoriale.

Composizione vettoriale

Dati quindi due numeri scalari a e b, e due vettori e , si definisce composizione vettoriale l'insieme di operazioni:

= a + b

che restituisce un nuovo vettore composto grazie alle operazioni di prodotto per uno scalare e somma vettoriale.
In particolare, se i vettori e non sono paralleli, è possibile dimostrare che scegliendo opportunamente gli scalari a e b è possibile ottenere qualsiasi vettore dello spazio .
Se quindi si sceglie una base unitaria ortonormale (, ) avente origine nel punto 0 di un sistema di assi cartesiani ortogonali a cui i versori sono collineari ed equiversi (cioè aventi uguale direzione e medesimo verso degli assi), si può facilmente verificare che: dato un punto P di coordinate (p₁, p₂), il vettore può essere ottenuto attraverso la composizione vettoriale a partire dalle basi come:

= p₁ + p₂ .

Allo stesso modo, in uno spazio vettoriale a tre dimensioni, stabilita una base a tre vettori non complanari è possibile comporre qualunque vettore.

Componenti di un vettore

Ciò permette di rappresentare qualunque vettore piano attraverso una coppia di numeri reali, che prendono il nome di componenti del vettore.
In termini formali, quindi, è possibile scrivere che:

.

In uno spazio a tre dimensioni occorreranno invece tre scalari.

Scomposizione vettoriale

Il processo inverso, quello che permette di partire da un vettore e di ricavare gli scalari, è invece detto decomposizione vettoriale o scomposizione vettoriale, e necessita di introdurre una nuova operazione, che prende il nome di prodotto scalare.

Prodotto scalare

Il prodotto scalare è un'operazione tra due vettori e che restituisce uno scalare a; si indica con il simbolo • (esempio: • ) o omettendo il simbolo (esempio: ), e si legge "scalare" (esempio: u scalare vi). Il risultato è uno scalare avente come valore il prodotto del modulo (della lunghezza) del primo vettore per il modulo del secondo per il coseno dell'angolo compreso tra i due.
Una semplice dimostrazione trigonometrica permette di verificare che il prodotto scalare può essere ottenuto, ad esempio, proiettando il primo vettore sulla direzione del secondo, poi se ne moltiplicano i moduli; oppure - il che è lo stesso - proiettando il secondo vettore sul primo, e poi moltiplicandone i moduli.
Il prodotto scalare quindi permette di determinare la proiezione di un vettore su una certa direzione n, semplicemente moltiplicando scalarmente il vettore per il versore della direzione n; se si utilizzano i versori e , si otterranno gli scalari v₁ e v₂ cercati. In termini formali:

.

Naturalmente, quando si passa ad uno spazio a tre dimensioni, la corrispondenza biunivoca si stabilisce tra terne di numeri reali e vettori tridimensionali.

Tensori

Dal punto di vista teorico, nulla vieta di costruire uno spazio vettoriale a partire da altri insiemi di scalari che non siano quello dei numeri reali, a condizione di definire adeguate operazioni di somma vettoriale e prodotto per uno scalare.
Proprio a partire da questa osservazione che è possibile costruire i tensori, enti vettoriali più complessi; se, infatti, si costruisce uno spazio vettoriale assumendo come insieme degli scalati proprio quello dei vettori precedentemente utilizzato, si otterranno una sorta di metavettori, cioè di "supervettori" le cui componenti non sono scalari ma vettori. Tale ente prende il nome di tensore del secondo ordine.
Allo stesso modo, se si utilizza lo spazio di tali tensori come insieme di scalari, si otterrà un nuovo ente che ha il nome di tensore del terzo ordine, un "super-supervettore" le cui componenti sono tensori di ordine 2, che a loro volta sono composti da vettori, e questi ultimi da scalari.
Il processo può essere reiterato per ottenere tensori di quarto, quinto, ennesimo ordine; si comprende anche che, applicando la medesima logica in senso opposto, sono classificati come tensori anche i vettori (di ordine uno) e gli stessi scalari (di ordine zero).

Voci correlate

La consultazione di TecnoLogica è preordinata alla lettura delle avvertenze