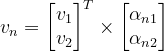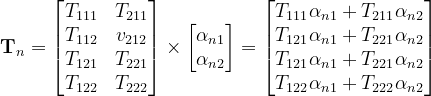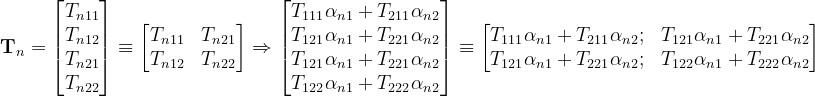Tensore

Da TecnoLogica.

Definizioni

Ente atto a individuare le grandezze geometriche e fisiche che obbediscono, per cambiamento di coordinate, a opportune leggi di trasformazione^[1].

Descrizione

Con il termine tensore si individua genericamente una struttura algebrica lineare capace di descrivere matematicamente un fenomeno fisico che è invariabile rispetto al sistema di riferimento adottato.
In altri termini, i tensori sono in grado di fornire quel supporto matematico che permette di rappresentare i processi che avvengono nel mondo reale, che sono indifferenti rispetto al punto di osservazione.
I tensori rappresentano quindi una famiglia di strutture algebriche molto ampia, e per tale motivo vengono raggruppati in ordini o tipi; ad esempio, un comune vettore è in realtà un tensore di ordine uno, mentre un semplice scalare può essere interpretato come un tensore di ordine zero.

Anche se i tensori sono indipendenti dal sistema di riferimento adottato, e quindi dalla loro rappresentazione, è di gran lunga più semplice ed utile comprenderne le potenzialità partendo proprio dalla loro espressione in componenti; per questo motivo, come primo approccio, è conveniente considerare le entità tensoriali in uno spazio dotato di assi coordinati ortogonali.
In generale, i tensori possono essere costruiti a partire da un numero qualsiasi di dimensioni, e quindi sono applicabili ad un generico spazio . Nelle applicazioni correnti della meccanica i tensori sono riferiti esclusivamente a spazi a tridimensionali; in numerosi casi è addirittura possibile costruire dei modelli nel piano, per cui i tensori si riducono ancora di dimensioni (e lo spazio di riferimento è ). La possibilità di utilizzare tensori piani è senz'altro più comoda nella comprensione di queste complesse strutture algebriche, perché ne semplifica notevolmente la rappresentazione, e per questo sarà adottata nelle successive spiegazioni; ciò non toglie nulla alla generalità delle dimostrazioni, che possono essere estese a tre, quattro o più dimensioni.

Vettori

I vettori sono un particolare tipo di tensore di primo ordine. Secondo la comune concezione, i vettori sono associati alla loro rappresentazione, cioè sono concepiti come dei segmenti orientati, applicati in un punto (di solito coincidente con l'origine degli assi) ed espressi attraverso delle componenti, che sono due nel caso di vettori piani e tre nel caso di vettori spaziali.
Ogni volta che il sistema di assi viene ruotato, le componenti cambiano secondo la legge di trasformazione dei vettori, che può geometricamente essere interpretata come la proiezione del vettore sul nuovo sistema.
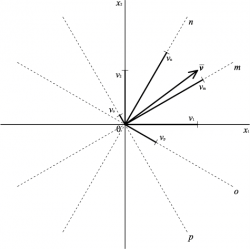
Secondo un approccio di tipo tensoriale il vettore può essere interpretato in modo diverso: esso è una funzione matematica lineare che associa ad ogni direzione del piano un numero scalare: se il vettore è denominato con , lo scalare associato alla direzione coordinata x₁ è indicato come v₁, mentre quello associato a x₂ è indicato come v₂.
Se si tracciano altre rette m, n, o, p…, il vettore associerà ad esse altri scalari: v_m, v_n, v_o, v_p, …; il modo con cui vengono stabiliti questi valori è appunto la legge di variazione dei vettori, e la loro interpretazione geometrica resta la proiezione del vettore sulla direzione. Dal punto di vista matematico però, al di là delle interpretazioni geometriche e delle rappresentazioni, un vettore è un ente algebrico che, ogni volta che si stabilisce una direzione nello spazio, associa ad essa uno scalare.
Assegnare una direzione significa assegnare il suo versore, e cioè il suo vettore unitario: questo è esprimibile attraverso una coppia (o terna, nel caso di uno spazio a tre dimensioni) di coseni direttori, e cioè con una coppia (o terna) di scalari.
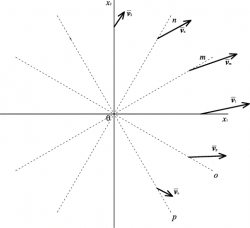
Detta n la generica direzione, il suo versore, e α_n1 e α_n2 i coseni direttori, il valore v_n che gli si associa è semplicemente determinabile grazie al prodotto scalare:

;

in termini matriciali, il prodotto è esprimibile come:

,

ed, infine, in termini di singola componente:

.

Un vettore quindi è una funzione algebrica lineare in grado di associare ad ogni direzione (e quindi ad ogni versore) uno scalare tramite il prodotto scalare.

Tensori doppi

I tensori doppi, o di secondo ordine, sono delle strutture algebriche più complesse dei vettori; per questo motivo, mentre i vettori possono godere di una doppia interpretazione (segmeti orientati oppure funzioni algebriche), questo tipo di tensori possono essere compresi solo dal punto di vista della funzione. Al contrario dei vettori, i tensori doppi non associano uno scalare ad una retta, ma un vettore vero e proprio, che non necessariamente deve essere allineato alla direzione di appartenenza.
Anche in questo caso, i vettori da associare alle diverse direzioni sono assegnati seguendo la relativa legge di trasformazione; in generale, ad ogni direzione viene assegnato un vettore diverso, sia in modulo che per l'orientamento.
Dato quindi un sistema di riferimento ed un tensore doppio , esso associerà un vettore ad ogni asse coordinato x_j. Nel caso piano, all'asse x₁ sarà assegnato il vettore , ed all'asse x₂ il vettore , con ≠ .
Se poi si tracciano altre rette m, n, o, p…, il tensore associerà ad esse altri vettori: , , , , …, sempre utilizzando la legge di trasformazione.
Un tensore doppio quindi è un ente matematico che, ogni volta che si stabilisce una direzione nello spazio, associa ad essa un vettore.
Dato che ad ogni asse coordinato x_i viene associato un vettore , il tensore doppio può essere considerato una sorta di metavettore, cioè un vettore le cui componenti non sono scalari, ma vettori stessi. In tal caso può essere espresso in forma matriciale come:

;

assegnare un vettore nel piano (o nello spazio) equivale a indicare le sue due (o tre) componenti; un tensore può quindi essere rappresentato da una matrice che raccoglie le componenti dei diversi assi coordinati. In altre parole, un tensore doppio del piano si indica con la notazione:

,

che invece nello spazio diventa:

.

Nella prima colonna della matrice sono raccolte le due (o tre) componenti del vettore associato all'asse x₁: v₁₁ è la componente in direzione x₁, mentre v₁₂ è la componente in direzione x₂. Se il tensore è nello spazio , allora v₁₃ è la componente in direzione x₃. La seconda colonna invece raggruppa le componenti del vettore associato a x₂, e così via.
In generale, v_ij è la componente in direzione x_j del vettore associato all'asse x_i.

Grazie alla notazione matriciale, è possibile sapere come calcolare facilmente il vettore da assegnare ad una generica direzione. Detta n la direzione, il suo versore, e α_n1 e α_n2 i coseni direttori, il vettore che gli si associa è semplicemente determinabile grazie al prodotto a destra di una matrice per un vettore:

;

in termini matriciali, il prodotto è esprimibile come:

,

ed, infine, in termini di singola componente:

.

Un tensore doppio quindi è una funzione algebrica lineare in grado di associare ad ogni direzione (e quindi ad ogni versore) un altro vettore tramite il prodotto a destra.

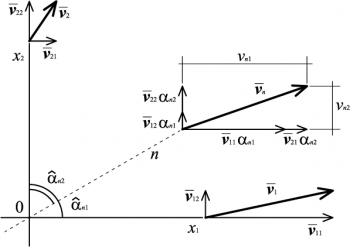
L'interpretazione geometrica è semplice: tutte le componenti in direzione x₁ (cioè i vettori e ) vengono moltiplicati per i coseni direttori omologhi (rispettivamente α_n1 e α_n2); si ottengono così due vettori, sempre orientati orizzontalmente, pari a e , in modulo minori di quelli di partenza^[2]; la loro somma restituisce il vettore , componente orizzontale del vettore associato alla direzione n. Lo stesso discorso può essere ripetuto per la direzione x₂, ed esteso alla direzione x₃ nel caso di tensori doppi nello spazio .

Tensori di ordine superiore al secondo

I tensori di ordine superiore al secondo non sono molto utilizzati nella meccanica e nella scienza delle costruzioni; la loro comprensione quindi può essere limitata agli aspetti fondamentali che regolano il loro comportamento, e dovrebbe essere condotta solo dopo aver preso dimestichezza con il concetto di tensore doppio. Essi infatti sono degli enti algebrici di complessità crescente, ma la loro struttura è del tutto simile a quella dei vettori e dei tensori doppi.

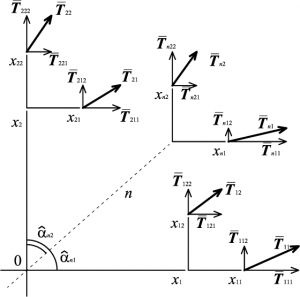
Immediatamente successivi ai tensori doppi, si trovano i tensori del terzo ordine: questi possono essere considerati come dei meta-meta vettori, che associano ad ogni direzione un tensore doppio. Detti T₁ e T₂ i tensori doppi associati agli assi x₁ e x₂, il tensore di terzo ordine potrebbe formalmente essere espresso come:

;

ogni volta che si traccia una direzione nello spazio, l'ente associa ad essa un tensore doppio seguendo la relativa legge di variazione.
Ciò equivale a dover immaginare di assegnare ad ogni asse coordinato un insieme di due (o tre, nel caso spaziale) sotto direzioni coordinate: sull'asse x₁ ci saranno le direzioni x₁₁ e x₁₂, e sull'asse x₂ ci saranno le direzioni x₂₁ e x₂₂. Ad ogni sub direzione si associa un vettore: e per le direzioni x₁₁ e x₁₂, e e per le direzioni x₂₁ e x₂₂. Così, il tensore di terzo ordine può essere scritto nel seguente modo:

,

cioè è esprimibile come una sorta di meta tensore doppio, un tensore doppio che ha per componenti dei vettori al posto degli scalari.

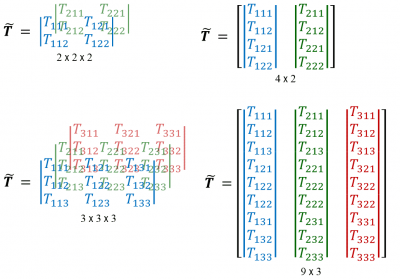
La rappresentazione matriciale in componenti richiederebbe di poter scrivere delle matrici nello spazio, cioè a forma di cubo: di dimensioni 2 x 2 x 2 nel caso piano, e di dimensioni 3 x 3 x 3 in quello spaziale.
È evidente che questa notazione è impraticabile: per questo motivo è necessario riferirsi a matrici piane di forma 4 x 2 e 9 x 3 costruite nel seguente modo:

• le colonne raggruppano le componenti dei tensori associati a un singolo asse: nella prima colonna ci sono le componenti del tensore T'₁ associato a x₁, nella seconda quelle di T₂ associato a x₂, e via di seguito; il primo dei tre indici (i, se Tijh è il generico termine) indica l'appartenenza all'asse;
• le prime due (o tre) righe della prima colonna raccolgono le componenti del vettore 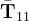associato al primo sub asse x₁₁, quelle della seconda colonna invece annoverano le componenti del vettore 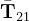associato a x₂₁, e così via; il secondo dei tre indici (j<, se T_ijh è il generico termine) individua quindi la sub direzione associata alla direzione coordinata indicata dal primo (i, se T_ijh è il generico termine);
• il singolo termine della matrice rappresenta una componente del generico vettore associato ad una delle quattro (o nove, nel caso spaziale) sub-direzioni; la componente è individuata dal terzo indice (h, se T_ijh è il generico termine, e rappresenta la componente del vettore 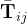lungo la direzione x_h).

Grazie alla notazione matriciale, è possibile sapere come calcolare facilmente il tensore doppio da assegnare ad una generica direzione. Detta n la direzione, il suo versore, e α_n1 e α_n2 i coseni direttori, il tensore doppio T_n che gli si associa è semplicemente determinabile grazie al prodotto a destra di una matrice per un vettore:

;

in termini matriciali, il prodotto è esprimibile come:

;

secondo la convenzione adottata per rappresentare matricialmente i tensori di terzo ordine, dovrà intendersi che sussiste la seguente equivalenza notazionale:

;

ed, infine, in termini di singola componente:

.

Un tensore di terzo ordine quindi è una funzione algebrica lineare in grado di associare ad ogni direzione (e quindi ad ogni versore) un altro tensore doppio tramite il prodotto a destra.
Il Tensore di Ricci è un tensore notevole del terzo ordine, le cui componenti sono spesso utilizzate nelle formule riguardanti i tensori.

(da completare)

Voci correlate

• Legge di trasformazione dei tensori

Note

1. ↑ Voce tensore dell'Enciclopedia on line Treccani.
2. ↑ Questo perché entrambi i vettori 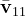e 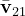vengono moltiplicati per i coseni direttori α_n1 e α_n2; i coseni direttori sono dei numeri compresi tra -1 e 1 (perché il coseno di qualsiasi angono è un valore compreso nell'intervallo [-1, 1]): ne consegue che il prodotto del vettore per uno scalare minore di uno sortisce un vettore di lunghezza minore di quello di partenza.

La consultazione di TecnoLogica è preordinata alla lettura delle avvertenze Ogni contributore è responsabile dei propri inserimenti. Il progetto è opera di Luca Buoninconti © 2011-2024.