Sezione in calcestruzzo armato/Pressoflessione

Da TecnoLogica.

Questa pagina contiene una o più parti ancora in corso di compilazione. Queste sono segnalate dalle diciture da compilare e/o da completare.

I contributori si impegnano a rendere disponibile e completo il lemma nel più breve tempo possibile.

Descrizione

(da compilare)

Progetto

(da compilare)

Verifica di una sezione rettangolare

Sia data una sezione in calcestruzzo armato rettangolare di dimensioni $LaTeX: b$ x $LaTeX: h$ , con armatura superiore compressa di area $LaTeX: A'_s$ , ed inferiore di area $LaTeX: A_s$ ; siano poi $LaTeX: d'$ e $LaTeX: d$ le rispettive distanze dal bordo superiore, e $LaTeX: d'' = h - d$ la distanza di $LaTeX: A_s$ dal bordo inferiore. Siano infine, entrambi noti, $LaTeX: N_{ud}$ e $LaTeX: M_{ud}$ lo sforzo normale di compressione [kN] ed il momento flettente [kN m] tale da comprimere le fibre superiori della sezione.
La verifica a pressoflessione viene condotta nel seguente modo:

scrivendo l'equazione di equilibrio alla traslazione, in cui compare lo sforzo normale $LaTeX: N_{ud}$ , si stabilisce la distanza $LaTeX: x$ dell'asse neutro dal bordo superiore;
scrivendo l'equilibrio alla rotazione si calcola il momento ultimo $LaTeX: M_{u}$ di rottura della sezione;
si confrontano i momenti $LaTeX: M_{ud}$ e $LaTeX: M_{u}$ : se risulta che $LaTeX: M_{ud}$ ≤ $LaTeX: M_{u}$ , allora la sezione è verificata.

Si procede nel seguente modo: si scrive quindi l'equilibrio alla traslazione, che formalmente assume la forma:

$LaTeX: F_c + F'_s - F_s = N_{ud}$ ,

avendo posto:

$LaTeX: F_c$ la risultante delle tensioni di compressione del calcestruzzo armato;
$LaTeX: F'_s$ la risultante delle tensioni di compressione del ferro posto nella parte superiore;
$LaTeX: F_s$ la risultante delle tensioni di trazione del ferro posto nella parte superiore.

Come già detto, $LaTeX: N_{ud}$ è lo sforzo normale che agisce sulla sezione. L'equazione di equilibrio è stata scritta ipotizzando che il bordo superiore della sezione è compresso, e quello inferiore è teso; in altri termini si ipotizza che la rottura avvenga tra i campi 2 e 4.
Secondo questa ipotesi il calcestruzzo è parzializzato (l'asse neutro infatti al massimo tange la sezione sul bordo inferiore). In particolare, se la rottura dovesse avvenire in campo 3, sia il calcestruzzo che il ferro si troverebbero in fase plastica. Se l'ipotesi fosse valida, l'equazione di equilibrio diventerebbe:

$LaTeX: 0.8 f_{cd} b x + f_{yd} A'_s - f_{yd} A_s = N_{ud}$ ,

dove:

$LaTeX: F_c = 0.8 f_{cd} b x$ ; il valore è ottenuto utilizzano lo stress block e un coefficiente di riempimento β = 0.8; $LaTeX: f_{cd}$ è la resistenza di calcolo cilindrica a compressione del calcestruzzo espressa in kN/cm²;
$LaTeX: F'_s = f_{yd} A'_s$ ; si considra il ferro compresso completamente plasticizzato;
$LaTeX: F_s = f_{yd} A_s$ ; si considra il ferro teso completamente plasticizzato.

In tal caso la profondità dell'asse neutro sarebbe:

$LaTeX: x = \frac {f_{yd} \left( A_s - A'_s \right) + N_{ud}} {0.8 f_{cd} b}$

,

e la profondità adimensionale dell'asse neutro ξ varrebbe:

$LaTeX: \xi = \frac{x}{d} = \frac {f_{yd} \left( A_s - A'_s \right) + N_{ud}} {0.8 f_{cd} b d}$

.

Ora sono logicamente possibili due alternative:

la rottura avviene effettivamente nel campo 3, per cui sia il valore di x che quello di ξ sono corretti, e si può procedere a calcolare il momento ultimo $LaTeX: M_u$ ;
la rottura avviene in altri campi, per cui occorre riscrivere l'equilibrio alla traslazione per trovare il valore corretto di x; solo dopo si potrà calcolare $LaTeX: M_u$ e completare la verifica.

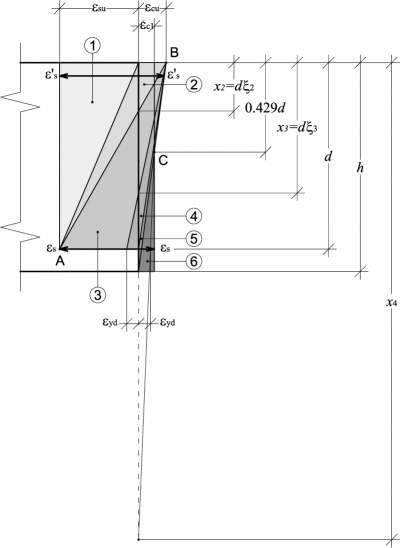
Per capire il campo di rottura si utilizza il valore di ξ precedentemente trovato, che rappresenta l'indicatore grazie al quale si stabilisce il modo con cui la sezione giunge a collasso.

Rottura in campo 2

Se ξ ≤ ξ₂, la rottura della sezione avviene in campo 2.
Il valore ξ₂ è infatti la profondità adimensionale dell'asse neutro posto al limite tra i campi 2 e 3; tale valore è indipendente dall'armatura, e vale ⁷/₂₇ = 0.259.
In campo 2 avviene che:

l'armatura inferiore $LaTeX: A_s$ è plasticizzata, cioè ε_s = 10⁰/₀₀ ≥ ε_yd, dove ε_s è l'allungamento del ferro e ε_yd è la deformazione al limite elastico dell'acciaio;
l'armatura superiore $LaTeX: A'_s$ può essere sia in campo elastico che plastico;
il calcestruzzo è parzializzato, e il suo allungamento massimo ε_cmax può essere sia in campo elastico che in quello plastico.

Per semplicità, si considererà solo il caso del calcestruzzo in campo plastico, perché molto più frequente. Questo permette di ridurre la verifica in campo 2 a soli due casi, e cioè:

$LaTeX: A'_s$ è in campo elastico, e occorre ricalcolare il valore di x (perché quello precedentemente ottenuto ipotizzava $LaTeX: A'_s$ plasticizzata);
$LaTeX: A'_s$ è in campo elastico, e il valore di x è corretto, e si può procedere a calcolare il momento ultimo.

Per capire in quale dei due precedenti casi si trova la sezione, occorre calcolare ε'_s utilizzando la relazione:

$LaTeX: \epsilon '_s = \epsilon _{cu} \frac{x - d'}{x} = 0.0035 \frac{x - d'}{x} = 0.0035 \frac{\xi - \delta }{\delta}$ ;

questa rappresenta l'accorciamento dell'acciaio se la rottura avviene sul limite di separazione tra i campi 2 e 3, quando la deformazione massima del calcestruzzo è ε_cmax = ε_cu = 3.5 ⁰/₀₀ = 0.0035, cioè ha raggiunto il valore di deformazione limite a compressione. Il valore δ = d'/d dipende dalla geometria della sezione, mentre ξ è quanto ottenuto dalla relazione (2).
Se dovesse verificarsi che ε'_s < ε_yd, allora l'acciaio superiore è in fase elastica, e il valore di x ottenuto con la (1) non è corretto. Deve quindi riscriversi l'equazione di equilibrio alla traslazione come:

$LaTeX: 0.8 f_{cd} b x + \alpha '_s f_{yd} A'_s - f_{yd} A_s = N_{ud}$ ,

dove però occorre preventivamente calcolare α'_s come:

$LaTeX: \alpha '_s = \frac {\sigma '_s} {f_yd} = \frac {\epsilon '_s} {\epsilon_{yd}}$ ;

vista la linearità del diagramma ε delle deformazioni, e non considerando che deve verificarsi che ε_s ≤ ε_su = 0.01^[1], è possibile porre:

$LaTeX: \epsilon '_s = \epsilon _{cu} \frac {x - d'} {x}$ ,

da cui si ricava:

$LaTeX: \alpha '_s = \epsilon _{cu} \frac {x - d'} {x} \frac {E_s} {f_{yd}} = 0.0035 \frac {x - d'} {x} \frac {20600} {f_{yd}} = \frac {72.1} {f_{yd}} \frac {x - d'} {x}$ .

Sostituendo α'_s nell'equazione di equilibrio e riarrangiandola algebricamente si ottiene:

$LaTeX: 0.8 f_{cd} b x^2 + \left(72.1 A'_s - f_{yd} A_s - N_{ud} \right) x - 72.1 A'_s d' = 0$ ,

la cui soluzione positiva è:

$LaTeX: x = 0.5 \left( -\alpha + \sqrt {\alpha ^2 + 4 \alpha'} \right)$

,

con:

$LaTeX: \alpha = \frac {72.1 A'_s - f_{yd} A_s - N_{ud}}{0.8 f_{cd} b}$ ,

$LaTeX: \alpha' = \frac {72.1 A'_s d'}{0.8 f_{cd} b}$ .

In entrambi i casi, sia se x è stato ottenuto con la (1) sia se è stata utilizzata la relazione (3), si calcola il momento ultimo $LaTeX: M_u$ rispetto al baricentro geometrico della sezione^[2], e cioè pari a:

$LaTeX: M_u = M'_u + N_{ud} \left( d'' - \frac {h}{2} \right)$

,

dove:

$LaTeX: M'_u = 0.8 f_{cd} b x \left( d - 0.4 x \right) + \alpha '_s f_{yd} A'_s \left(d - d' \right)$

,

avendo posto α'_s pari a 1 se x è stato ottenuto con la (1), e pari a 72.1 (x-d')/(f_yd x) se x è stato ottenuto con la (3).

La sezione risulta quindi verificata se $LaTeX: M_{ud}$ ≤ $LaTeX: M_u$ .

Rottura in campo 3

Se ξ₂ ≤ ξ ≤ ξ₃, la rottura della sezione avviene in campo 3.
In questo caso, il valore ξ₃ dipende dal tipo di acciaio utilizzato, e vale:

0.688 per acciaio tipo FeB38K;
0.658 per acciaio tipo FeB44K.

Se la rottura avviene in campo 3, il valore di x trovato con la (1) è corretto; per tale motivo il momento ultimo $LaTeX: M_u$ può essere calcolato, come in campo 2, con la relazione (4), avendo valutato $LaTeX: M'_u$ utilizzando la relazione (5) con α'_s pari a 1.

La sezione risulta quindi verificata se $LaTeX: M_{ud}$ ≤ $LaTeX: M_u$ .

Rottura in campo 4

Se ξ₃ ≤ ξ ≤ 1, la rottura della sezione avviene in campo 4.
In questo caso, il valore ξ₃ dipende dal tipo di acciaio utilizzato, e vale:

0.688 per acciaio tipo FeB38K;
0.658 per acciaio tipo FeB44K.

Quando ciò accade, l'armatura inferiore è tesa e l'acciaio è in campo elastico, e quindi ε_s < ε_yd.
In teoria, l'armatura superiore compressa potrebbe essere tanto in campo elastico quanto in campo plastico. Per essere in campo elastico, l'armatura dovrebbe essere abbastanza lontana dal bordo superiore; sfruttando la linearità del diagramma di ε, dovrebbe infatti verificarsi che d' > ³/₇ x: questa condizione è però veramente molto remota. Con grande probabilità quindi il ferro compresso è plasticizzato, e l'equazione di equilibrio alla traslazione diventa:

$LaTeX: 0.8 f_{cd} b x + f_{yd} A'_s - \alpha_s f_{yd} A_s = N_{ud}$ ,

dove però occorre preventivamente calcolare α_s come:

$LaTeX: \alpha _s = \frac {\sigma _s} {f_yd} = \frac {\epsilon _s} {\epsilon_{yd}}$ ;

vista la linearità del diagramma ε delle deformazioni, è possibile porre:

$LaTeX: \epsilon _s = \epsilon _{cu} \frac {x - d} {x}$ ,

da cui si ricava:

$LaTeX: \alpha _s = \epsilon _{cu} \frac {x - d} {x} \frac {E_s} {f_{yd}} = 0.0035 \frac {x - d} {x} \frac {20600} {f_{yd}} = \frac {72.1} {f_{yd}} \frac {x - d} {x}$

.

Sostituendo α_s nell'equazione di equilibrio e riarrangiandola algebricamente si ottiene:

$LaTeX: 0.8 f_{cd} b x^2 + \left( f_{yd} A'_s - 72.1 A_s - N_{ud} \right) x - 72.1 A_s d = 0$ ,

la cui soluzione positiva è analoga alla (3), dove però:

$LaTeX: \alpha = \frac { f_{yd} A'_s - 72.1 A_s - N_{ud}}{0.8 f_{cd} b}$ ,

$LaTeX: \alpha' = \frac {72.1 A_s d}{0.8 f_{cd} b}$ .

Le relazioni (4) e (5) consentono di calcolare il momento ultimo $LaTeX: M_u$ .

La sezione risulta quindi verificata se $LaTeX: M_{ud}$ ≤ $LaTeX: M_u$ .

Rottura in campo 5

Se 1 ≤ ξ ≤ λ' la rottura della sezione avviene in campo 5.
Il valore λ' = h/d. In altre parole, per ξ = λ' l'asse neutro tocca il bordo inferiore della sezione.
Nel campo 5 entrambe le armature sono compresse; come in campo 4, anche qui è plausibile considerare che l'armatura superiore sia in fase plastica (per non esserlo, dovrebbe essere d' > ³/₇ x) mentre certamente quella inferiore è in campo elastico.
L'equazione alla traslazione diventa:

$LaTeX: 0.8 f_{cd} b x + f_{yd} A'_s + \alpha_s f_{yd} A_s = N_{ud}$

,

dove α_s si calcola utilizzando la relazione (6).

Sostituendo α_s nell'equazione di equilibrio e riarrangiandola algebricamente si ottiene:

$LaTeX: 0.8 f_{cd} b x^2 + \left( f_{yd} A'_s + 72.1 A_s - N_{ud} \right) x - 72.1 A_s d = 0$ ,

la cui soluzione positiva è analoga alla (3), dove però:

$LaTeX: \alpha = \frac { f_{yd} A'_s + 72.1 A_s - N_{ud}}{0.8 f_{cd} b}$ ,

$LaTeX: \alpha' = \frac {72.1 A_s d}{0.8 f_{cd} b}$ .

Il momento ultimo si può calcolare direttamente utilizzando la relazione:

$LaTeX: M_u = 0.8 f_{cd} b x \left( \frac {h}{2} - 0.4 x \right) + f_{yd} A'_s \left( \frac {h}{2} - d' \right) - \alpha _s f_{yd} A_s \left( \frac {h}{2} - d \right)$

.

La sezione risulta quindi verificata se $LaTeX: M_{ud}$ ≤ $LaTeX: M_u$ .

Rottura in campo 6

Se ξ ≥ λ' la rottura della sezione avviene in campo 6.
L'asse neutro è esterno alla sezione, che risulta tutta compressa.
In campo 6, la deformazione masssima del calcestruzzo ε_cmax varia da un massimo di ε_cu = 3.5 ⁰/₀₀ = 0.0035 (quando x = h, cioè l'asse neutro tange il bordo inferiore della sezione) ad un minimo di ε_c1 = 2 ⁰/₀₀ = 0.002 (quando x è all'infinito, e la sezione è soggetta esclusivamente a sforzo normale). Il calcestruzzo non è parzializzato, cioè tutta la superficie della sezione reagisce a compressione. Il diagramma σ delle tensioni è del tipo "parabola-rettangolo"; dato però che l'asse neutro è esterno alla sezione, il ramo parabolico progressivamente scompare mano a mano che l'asse neutro si allontana, fino a svanire completamente nel caso limite di asse all'infinito. Questo significa che il coefficiente di riempimento β varia da un minimo di 0.8 (limite tra i campi 4 e 5) ad un massimo di 1.0.
Per evitare calcoli complessi, il campo 6 può essere diviso in tre sottocampi, caratterizzati da diversi valori di β e di α_s (infatti anche l'armatura inferiore, inizialmente in campo elastico, evolve verso la fase plastica all'allontanarsi di x), e cioè:

primo sottocampo: β = 0.8 e ε_s ≤ ε_yd;
secondo sottocampo: β = 1.0 e ε_s ≤ ε_yd;
terzo sottocampo: β ≤ 1.0 e ε_s > ε_yd.

Primo sottocampo

Se λ' ≥ ξ ≥ 1.25 λ' la rottura avviene nel primo sottocampo.
Per la semplificazione adottata, β = 0.8 e α'_s = 1 (armatura superiore in campo plastico)^[3]. Il valore di α_s può essere trovato sftuttando la linearità del diagramma delle ε deformazioni. Sapendo che il pivot C si trova a ³/₇h dal bordo superiore (x_c = ³/₇h) e che dista di ε_c1 dalla sezione, è possibile scrivere la relazione:

$LaTeX: \frac{\epsilon_s}{x-d} = \frac{\epsilon_{c1}}{x-x_c} \Rightarrow \epsilon_s = \frac{7}{500} \frac{x-d}{7x - 3h}$ ,

da cui:

$LaTeX: \alpha_s = \frac{\epsilon_s}{\epsilon_{yd}} = \epsilon_s \frac{E_s}{f_{yd}} = \frac{288.4}{f_{yd}} \frac{x-d}{7x - 3h}$

.

L'equazione di equilibrio alla traslazione è analoga alla (7), e la sua soluzione positiva è analoga alla (3) dove però:

$LaTeX: \alpha = \frac{7 f_{yd} A'_s - 2.4 f_{cd} b h + 288.4 A_s - 7 N_{ud}}{5.6 f_{cd} b}$

$LaTeX: \alpha' = \frac{3 f_{yd} A'_s h + 288.4 A_s d - 3 N_{ud} h}{5.6 f_{cd} b}$ .

Il momento ultimo si può calcolare direttamente utilizzando la relazione (8).
La sezione risulta quindi verificata se $LaTeX: M_{ud}$ ≤ $LaTeX: M_u$ .

Secondo sottocampo

Se 1.25 λ' ≤ ξ ≤ x₄/d la rottura avviene nel secondo sottocampo.
Per la semplificazione adottata, β = 1 e α'_s = 1. L'armatura inferiore è ancora in campo plastico, in quanto il valore x₄ rappresenta appunto la profondità massima dell'asse neutro superata la quale anche l'acciaio nel bordo inferiore si plasticizza.
Il valore di x₄ può essere trovato utilizzando la linearità del diagramma ε delle deformazioni:

$LaTeX: x_4 = \frac{2884 d - 3 f_{yd} d}{7 \left( 412 - f_{yd} \right) }$

che può essere scritta in funzione del tipo di acciaio, e cioè:

per FeB38K, $LaTeX: x_4 = \frac {1442 \lambda - 489}{301} h$ ,

per FeB44k, $LaTeX: x_4 = \frac {1442 \lambda - 561}{133} h$ ,

dove λ = d/h.
Il valore α_s può essere trovato usando la relazione (9). Si scrive quindi l'equilibrio alla traslazione come:

$LaTeX: f_{cd} b h + f_{yd} A'_s + \alpha_s f_{yd} A_s = N_{ud}$ ;

sostituito quindi α_s, la soluzione dell'equazione di primo grado comporta:

$LaTeX: x = \frac {3 f_{cd} b h^2 + 3 f_{yd} A'_s h + 288.4 A_s d - 3 N_{ud}}{7 f_{cd} b h + 7 f_{yd} A'_s + 288.4 A_s - 7 N_{ud}}$ .

Il momento ultimo si può calcolare direttamente utilizzando la relazione (8).
La sezione risulta quindi verificata se $LaTeX: M_{ud}$ ≤ $LaTeX: M_u$ .

Terzo sottocampo

Se ξ > x₄/d, la rottura avviene nel terzo sottocampo.
In questo caso, anche l'acciaio teso entra in fase plastica, e l'equilibrio alla traslazione diventa:

$LaTeX: \beta f_{cd} b h + f_{yd} A'_s + f_{yd} A_s - N_{ud} = 0$ ;

grazie a questa relazione, è possibile calcolare il valore:

$LaTeX: \beta = \frac{N_{ud} - f_{yd} \left(A'_s - A_s \right) }{f_{cd} b h}$ .

Sapendo che poi, approssimativamente, la relazione che lega $LaTeX: \beta$ e $LaTeX: x$ è pari a:

$LaTeX: \beta = \frac{x - 0.8 h}{x - 0.75 h}$ ,

si ottiene la posizione dell'asse neutro ponendo:

$LaTeX: x = \frac{15 \beta -16}{\beta - 1} \frac{h}{20}$ ,

grazie alla quale è possibile calcolare il momento ultimo grazie alla relazione (8).
La sezione risulta quindi verificata se $LaTeX: M_{ud}$ ≤ $LaTeX: M_u$ .

Voci correlate

Sezione in calcestruzzo armato

Note

↑ Ciò equivale a considerare che l'acciaio abbia una duttilità infinita.
↑ Infatti, quando si risolve il telaio per determinare le sollecitazioni nelle aste (in questo caso sono lo sforzo normale $LaTeX: N_{ud}$ e $LaTeX: M_{ud}$ ) le armature non sono ancora note, e sia il baricentro che l'inerzia sono quelle riferite alla geometria della sezione; per questo motivo, gli quilibiri alla traslazione ed alla rotazione devono essere calcolati rispetto al baricentro geometrico, considerando quindi lo sforzo normale agente in questo punto, e non nel baricentro delle masse.
↑ Ciò equivale a considerare uno stress block ridotto di circa il 20% rispetto all'estensione reale. La semplificazione quindi è a vantaggio di sicurezza.

La consultazione di TecnoLogica è preordinata alla lettura delle avvertenze

[0] Ciò equivale a considerare che l'acciaio abbia una duttilità infinita.

[1] Infatti, quando si risolve il telaio per determinare le sollecitazioni nelle aste (in questo caso sono lo sforzo normale $LaTeX: N_{ud}$ e $LaTeX: M_{ud}$ ) le armature non sono ancora note, e sia il baricentro che l'inerzia sono quelle riferite alla geometria della sezione; per questo motivo, gli quilibiri alla traslazione ed alla rotazione devono essere calcolati rispetto al baricentro geometrico, considerando quindi lo sforzo normale agente in questo punto, e non nel baricentro delle masse.

[2] Ciò equivale a considerare uno stress block ridotto di circa il 20% rispetto all'estensione reale. La semplificazione quindi è a vantaggio di sicurezza.

[1]

[2]

[3]

Sezione in calcestruzzo armato/Pressoflessione

Da TecnoLogica.

Descrizione

Progetto

Verifica di una sezione rettangolare

Rottura in campo 2

Rottura in campo 3

Rottura in campo 4

Rottura in campo 5

Rottura in campo 6

Primo sottocampo

Secondo sottocampo

Terzo sottocampo

Voci correlate

Note

Visite

Strumenti personali

Navigazione

Ricerca

Strumenti