Rumore stradale
Da TecnoLogica.
|
Descrizione
(da compilare)
Calcolo
Metodo approssimato
Il paragrafo è un contributo orignale dell'autore
In prima approssimazione, il livello di rumore stradale può essere determinato dalla somma algebrica di:
- il rumore Lp prodotto dalla strada, determinato ad una distanza convenzionale di 10 metri dall'asse geometrico dell'infrastruttura;
- un incremento Δ Lp,1 dovuto all'eventuale pendenza;
- un incremento Δ Lp,2 dovuto al tipo di manto stradale;
- un decremento Δ Lp,gd dovuto alla reale distanza di ascolto;
- un decremento Δ Lp,va dovuto all'angolo di vista;
- un decremento Δ Lp,h dovuto alla eventuale presenza costruzioni;
- un decremento Δ Lp,fol dovuto alla eventuale presenza di vegetazione.
In totale, per ogni strada presente, il livello di pressione sonora è pari a:
Ltot = Lp + Δ Lp,1 + Δ Lp,2 - Δ Lp,gd - Δ Lp,va - Δ Lp,h - Δ Lp,fol.
Trovati i livelli totali per ogni strada, il rumore stradale totale è pari a:
In assenza di dati sul traffico dell'infrastruttura, è possibile utilizzare in via approssimativa e speditiva i seguenti valori di pressione sonora[1] per le strade extraurbane:
| Tipo di strada | TGM | Velocità | Livello di pressione sonora | |||
|---|---|---|---|---|---|---|
| pesante | leggero | pesante | leggero | min | max | |
| Autostrada (A) di grande traffico | 52000 | 260000 | 80 km/h | 110 km/h | 108 dB | 121 dB |
| Autostrada (A) | 14000 | 70000 | 80 km/h | 110 km/h | 102 dB | 116 dB |
| Strada extraurbana principale (B) a scorrimento veloce | 2500 | 25000 | 70 km/h | 90 km/h | 96 dB | 109 dB |
| Strada extraurbana principale (B) | 500 | 10000 | 60 km/h | 70 km/h | 89 dB | 102 dB |
I livelli di pressione sonora devono considerarsi valutati per una strada piana ed al bordo della carreggiata, ad una distanza di 10 metri dall'asse viario origne del rumore.
Per le strade urbane, l'intensità di traffico può essere ipotizzata in base alla fascia di antropizzazione, al tipo di strada ed alla larghezza della carreggiata. Distinguendo per semplicità solo due tipologie di larghezza, corrispondenti a sedi stradali di circa sei e dodici metri (all'incirca due e quattro corsie rispettivamente), è possibile determinare il rumore utilizzando la seguente tabella[2]:
| Fascia | Strada | |||
|---|---|---|---|---|
| Principale | Secondaria | |||
| larga | stretta | larga | stretta | |
| I | 51÷69 dB | 48÷66 dB | 44÷62 dB | 41÷59 dB |
| II | 52÷7 dB | 49÷67 dB | 46÷64 dB | 43÷61 dB |
| III | 58÷72 dB | 55÷69 dB | 51÷65 dB | 48÷62 dB |
| IVa | 59÷73 dB | 56÷70 dB | 53÷67 dB | 50÷64 dB |
| IVb | 61÷76 dB | 58÷73 dB | 54÷79 dB | 51÷66 dB |
| V | 63÷78 dB | 60÷75 dB | 56÷70 dB | 53÷67 dB |
Le coppie di valori si riferiscono ai livelli di pressione sonora massimo e minimo, e si riferiscono ai periodi diurno e notturno.
Nel caso in cui la pendenza della strada non sia nulla, i valori di cui sopra devono essere incrementati (Δ Lp,1) seguendo le indicazioni della seguente tabella:
| Pendenza | Incremento |
|---|---|
| <2% | 0 dB |
| 2 - 3% | 1 dB |
| 3 - 6% | 2 dB |
| 6 - 15% | 3 dB |
| >15% | 4 dB |
Un ulteriore incremento (Δ Lp,2)deve essere introdotto nel caso sia noto il tipo di manto stradale; la tabella di riferimento è la seguente:
| Manto stradale | Incremento |
|---|---|
| Asfalto liscio | 0 dB |
| Asfalto ruvido | 4 dB |
| Acciottolato | 7 dB |
Il rumore totale è dato quindi dalla somma del rumore stradale più i due incrementi; terminata questa fase, si procede a calcolare le attenuazioni, cioè le differenti aliquote che devono essere sottratte al totale precedentemente ottenuto.
In funzione delle semplificazioni adottate in questo metodo approssimato, è possibile considerare quattro tipi di attenuazione, calcolati come segue.
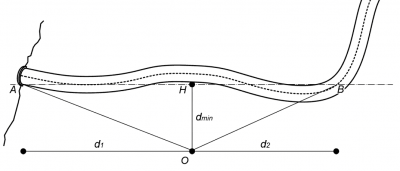
L'attenuazione dovuta alla divergenza geometrica (e cioè alla distanza dmin che separa il punto di ascolto rispetto al centro della strada è pari a:
Un'ulteriore attenuazione è dovuta all'angolo di vista: il livello di pressione sonora finora trovato si basa infatti sull'assunto teorico che l'infrastruttura si prolunghi indefinitamente, mentre essa nella realtà può curvare allontanandosi dal punto di ascolto, o può interrompersi per passare in galleria. Tale decremento è funzione dell'angolo AOB - dove O è il punto di ascolto - entro il quale è racchiusa la porzione di strada che produce quel livello di rumore che colpisce effettivamente l'osservatore. Conosciuta la distanza minima dmin} e le distanze d1 e d2 (vedi figura a lato), l'attenuazione è data dalla formula:
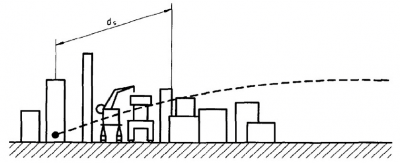
La terza aliquota è rappresentata dalla presenza di costruzioni che eventualmente si interpongono tra la linea stradale e l'ascoltatore. In tal caso, bisogna considerare che il suono, piuttosto che muoversi in linea retta, raggiunge il punto di ascolto seguendo una traiettoria curva, la cui parte iniziale può essere immaginata come una retta inclinata di circa 15° rispetto al piano orizzontale. Disegnata la sezione, è possibile vedere che questa traiettoria attraversa le costruzioni sia dal lato in cui si trova l'osservatore che dal lato della strada, per una distanza totale ds. Dopo aver determinato la distanza, bisogna stabilire la densità delle costruzioni attraversate dal suono; questa a sua volta è funzione della fascia di antropizzazione, come riportato nella seguente tabella:
| Fascia | I | II | III | IVa | IVb | V |
|---|---|---|---|---|---|---|
| Densità B | 0.10 | 0.30 | 0.50 | 0.50 | 0.65 | 0.80 |
Individuati i valori di densità dei luoghi vicini all'osservatore ed all'infrastruttura, se ne calcola la media B; ora è possibile determinare il valore di attenuazione cercato:
Δ Lp,h = 0.1 B ds .
L'ultima attenuazione è quella prodotta quando il suono passa attraverso la vegetazione. In realtà il suono perde di energia solo se gli alberi sono molto fitti e ravvicinati, altrimenti è scorretto applicare tale valore di riduzione. Concettualmente occorre eseguire il medesimo ragionamento fatto in precedenza, perché anche qui la traiettoria del rumore è curva con la stessa inclinazione iniziale di 15°. Trovata la distanza d = d1 + d2 percorsa dal segnale sonoro attraverso le chiome degli alberi, l'attenuazione è data dalla relazione:
Δ Lp,fol = d K,
dove il valore di K si deduce dalla seguente tabella:
| Distanza | K |
|---|---|
| < 20 m | 1 dB/m |
| ≥ 20 m | 0.04 dB/m |
Inoltre, se la distanza d supera i 200 metri, bisogna considerare un valore massimo di attenuazione di 8 dB.
Il rumore stradale finale è dato quindi dalla somma del rumore totale meno i valori di attenuazione precedentemente trovati.
Modelli di calcolo
I modelli di calcolo utilizzati in situazioni di traffico extraurbano sono[3]:
Questi permettono di valutare l'inquinamento acustico se si conosce il flusso di veicoli orario (valore indirettamente ricavabile quando è noto il traffico giornaliero medio) suddiviso in pesante e leggero, e la velocità media.
Voci correlate
Note
- ↑ La tabella e le modalità di determinazione del TGM, e quindi i livelli di pressione sonora calcolati, sono un contributo originale dell'autore. Cfr.[L. Buoninconti, Metodi di verifica della biocompatibilità nel progetto di architettura.]Luca Buoninconti (2010).
Metodi di verifica della biocompatibilità nel progetto di architettura. Un approccio integrale al comfort. UniNa. Show in Bibliography - ↑ La tabella e le modalità di valutazione sono un contributo originale dell'autore.
- ↑ Commissione Interaziendale ANAS, Ente Ferrovie dello Stato, Società Autostrade, AISCAT, Ministero del'Ambiente, Istruzioni per l'inserimento ambientale delle infrastrutture stradali e ferroviarie con riferimento al controllo dell'inquinamento acustico, ANAS, 1992.
|