Cerchio di Mohr/Dimostrazione

Da TecnoLogica.

Questa pagina contiene una o più parti ancora in corso di compilazione. Queste sono segnalate dalle diciture da compilare e/o da completare.

I contributori si impegnano a rendere disponibile e completo il lemma nel più breve tempo possibile.

Descrizione

Sia dato il tensore tensore di secondo ordine piano simmetrico $LaTeX: \mathbf{S}$ nelle sue componenti principali:

$LaTeX: \mathbf{S} = \begin{bmatrix} s_{I} & 0 \\ 0 & s_{II} \end{bmatrix}$ .

Ogni volta che si assegna una direzione n di coseni direttori (α_nI, α_nII), il tensore $LaTeX: \mathbf{S}$ associa ad essa un vettore $LaTeX: \bar {\mathbf{s}} _n$ di coordinate:

$LaTeX: s_{n1} = \alpha_{nI} s_I$ ,

$LaTeX: s_{n2} = \alpha_{nII} s_{II}$ .

Il tensore $LaTeX: \mathbf{S}$ può essere espresso come somma di due tensori, il primo sferico ( $LaTeX: \mathbf{C}$ ) ed il secondo deviatorico ( $LaTeX: \mathbf{R}$ ) di coordinate:

$LaTeX: \mathbf{C} = \begin{bmatrix} \frac{s_{I}+s_{II}}{2} & 0 \\ 0 & \frac{s_{I}+s_{II}}{2} \end{bmatrix} = \begin{bmatrix} C & 0 \\ 0 & C \end{bmatrix}$ ,

$LaTeX: \mathbf{R} = \begin{bmatrix} \frac{s_{I}-s_{II}}{2} & 0 \\ 0 & - \frac{s_{I}-s_{II}}{2} \end{bmatrix} = \begin{bmatrix} r & 0 \\ 0 & -r \end{bmatrix}$ .

È immediato verifcare come $LaTeX: \mathbf{S} = \mathbf{C} + \mathbf{R}$ .

Si osserva che il tensore sferico $LaTeX: \mathbf{C}$ , ogni volta che si assegna una direzione n di coseni direttori (α_nI, α_nII), associa ad essa un vettore $LaTeX: \bar {\mathbf{C}} _n$ di coordinate:

$LaTeX: C_{n1} = \alpha_{nI} C$ ,

$LaTeX: C_{n2} = \alpha_{nII} C$ .

Il modulo di questo vettore è pari a:

$LaTeX: \left|\bar {\mathbf{C}} _n \right| = C_n = \sqrt { \left( \alpha_{nI} C \right)^2 + \left( \alpha_{nII} C \right)^2 } = C \sqrt{\alpha_{nI}^2 + \alpha_{nII}^2 } = C$ .

Conosciuto il modulo, l'inclinazione del vettore $LaTeX: \bar {\mathbf{C}} _n$ è facilmente indivuduabile, perché i suoi coseni direttori $LaTeX: \bar {\mathbf{e}}_{CnI}$ e $LaTeX: \bar {\mathbf{e}}_{CnII}$ sono dati dal rapporto tra le sue componenti ed il modulo stesso, e cioè:

$LaTeX: \bar {\mathbf{e}}_{CnI} = \frac{C_{nI}}{C_n} = \frac{\alpha_{nI} C}{C} = \alpha_{nI}$ ,

$LaTeX: \bar {\mathbf{e}}_{CnII} = \frac{C_{nII}}{C_n} = \frac{\alpha_{nII} C}{C} = \alpha_{nII}$ .

Dato che il vettore $LaTeX: \bar {\mathbf{C}} _n$ e la direzione n hanno gli stessi coseni direttori, essi sono collineari, ovvero $LaTeX: \bar {\mathbf{C}} _n$ giace su n.
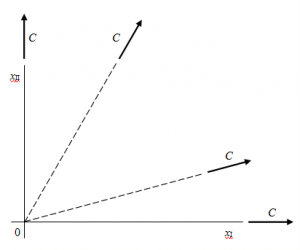
Questa prorietà è comune a tutti i tensori sferici: comunque si scelga una direzione nel piano, il tensore gli assegna un vettore collineare dello stesso modulo, pari alle componenti degli assi coordinati di riferimento.

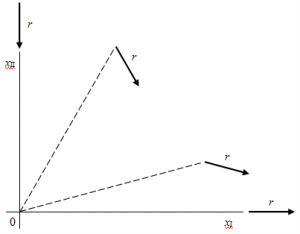
Per quanto riguarda la parte deviatorica $LaTeX: \mathbf{R}$ , ogni volta che si assegna una direzione n di coseni direttori (α_nI, α_nII), associa ad essa un vettore $LaTeX: \bar {\mathbf{r}} _n$ di coordinate:

$LaTeX: r_{n1} = \alpha_{nI} r$ ,

$LaTeX: r_{n2} = - \alpha_{nII} r$ .

Il modulo questa volta è pari a:

$LaTeX: \left|\bar {\mathbf{r}} _n \right| = r_n = \sqrt { \left( \alpha_{nI} r \right)^2 + \left( - \alpha_{nII} r \right)^2 } = r \sqrt{\alpha_{nI}^2 + \alpha_{nII}^2 } = r$ .

L'inclinazione del vettore $LaTeX: \bar {\mathbf{r}} _n$ si individua allo stesso modo come:

$LaTeX: \bar {\mathbf{e}}_{rnI} = \frac{r_{nI}}{r_n} = \frac{\alpha_{nI} r}{r} = \alpha_{nI}$ ,

$LaTeX: \bar {\mathbf{e}}_{rnII} = \frac{r_{nII}}{r_n} = \frac{- \alpha_{nII} r}{r} = - \alpha_{nII}$ .

Questa volta il secondo coseno direttore di $LaTeX: \bar {\mathbf{C}} _n$ e della direzione n differiscono di segno: questo significa che le loro inclinazioni sono opposte (se, ad esempio, n è inclinata di 15° rispetto all'asse x_I, allora $LaTeX: \bar {\mathbf{C}} _n$ è inclinato di -15° rispetto allo stesso asse, e così via).

Proseguendo, si ricorda che i tensori sferico e deviatorico sono stati costruiti in modo tale che $LaTeX: \mathbf{S} = \mathbf{C} + \mathbf{R}$ .
Per tale motivo, se si assegnano il tensore $LaTeX: \mathbf{S}$ ed una generica direzione n, il vettore ad essa associato dovrà essere tale che:

$LaTeX: \bar {\mathbf{s}} _n = \bar {\mathbf{C}} _n + \bar {\mathbf{r}} _n$ .

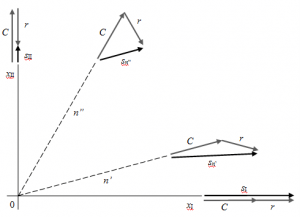
Si immagini quindi di prendere una direzione n, passante per l'origine, inizialmente coincidente con l'asse x_I; il vettore ad essa associato sarà naturalmente $LaTeX: \bar {\mathbf{s}} _I$ , che tra l'altro è ottenuto sommando la componente sferica C con quella deviatorica r.
Facendo ruotare la direzione intorno all'origine degli assi, la componente sferica resta giacente sulla direzione; al contrario, la parte deviatorica si separa dalla essa di un angolo proporzionale all'inclinazione della retta rispetto all'asse x_I; maggiore è la sua inclinazione, più elevato sarà questo angolo.
Se, ad esempio, la direzione è giunta nella posizione n', inclinata di 15° rispetto a x_I (vedi figura a lato), la componente deviatorica risulterà inclinata di -15° rispetto al medesimo asse (e quindi di 30° rispetto a n').
Analogamente, se n giunge nella posizione n", inclinata di 60°, la componente deviatorica sarà invece inclinata di -60° (e di conseguenza l'angolo formato tra n" e r sarà di 120°).
Ne consegue che, facendo ruotare n intorno all'origine degli assi, r ruoterà intorno a n, mentre C resterà fissa su n.

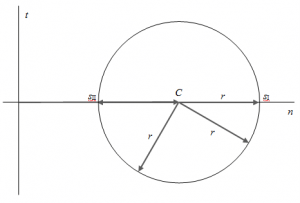
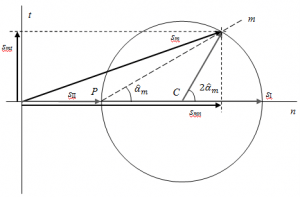
Si immagini ora di ripiegare tutte le infinite posizioni assunte da n, nel corso della sua rotazione intorno all'origine, sull'asse orizzontale: tutti i vettori C si sovrapporrebbero^[1], mentre le componenti deviatoriche r descriverebbero, a partire dall'estremo di C, una circonferenza, che è appunto il cerchio di Mohr.
In questo nuovo diagramma l'asse orizzontale è indicato con n , e t quello verticale, questo perché, come si vedrà più avanti, permettono di individuare le componenti normale e tangenziale del vettore $LaTeX: \bar {\mathbf{s}}_{m}$ associato ad una generica direzione m.
Il cerchio così costruito è quindi il luogo dei vertici di tutti i vettori r rappresentabili nel piano x_I0x_II. È quindi possibile pensare che ogni punto della circonferenza sia il secondo vertice del vettore somma di C ed r, il cui primo punto è l'origine deli sistema di assi n0t. Ma, dato che $LaTeX: \bar {\mathbf{C}} + \bar {\mathbf{r}} = \bar {\mathbf{s}}_n$ , si comprende che il cerchio di Mohr è anche il luogo dei vertici di tutti i vettori $LaTeX: \bar {\mathbf{s}}_n$ associabili alle infinite posizioni che la direzione n può assumere nel piano x_I0x_II. Sull'asse orizzontale i vettori individuati dal cerchio sono proprio $LaTeX: \bar {\mathbf{s}}_I$ e $LaTeX: \bar {\mathbf{s}}_{II}$ , associate alle direzioni x_I e x_II.

Il cerchio si presta per essere utilizzato in una costruzione geometrica che sia in grado di individuare il vettore da associare ad una generica direzione m, senza utilizzare la legge di trasformazione dei tensori. Per fare ciò occorre però trovare come tracciare sul diagramma di Mohr la direzione, e fare in modo che essa intersechi il cerchio nel punto che rappresenta esattamente il vettore $LaTeX: \bar {\mathbf{s}}_m$ ad essa assegnato dal tensore.
Si individua quindi un punto P detto polo del cerchio in questo modo: si traccia una retta orizzontale passante per l'estremo del vettore $LaTeX: \bar {\mathbf{s}}_I$ , poi una retta verticale passante per il vertice di $LaTeX: \bar {\mathbf{s}}_{II}$ ; l'intersezione delle due rette, che coincide con il vertice di $LaTeX: \bar {\mathbf{s}}_{II}$ , è il punto cercato.
Fissata quindi l'inclinazione $LaTeX: \hat {\alpha}_{m}$ della direzione m rispetto all'asse x_I, si traccia una retta a partire da P della medesima inclinazione rispetto all'asse n: questa incontra il cerchio in un punto, distinto da P, che rappresenta il vertice del vettore $LaTeX: \bar {\mathbf{s}}_m$ ; il suo punto iniziale invece è, come di consueto, l'origine degli assi.
Si noti inoltre che la componente deviatorica del vettore è inclinata rispetto all'asse m di un angolo pari a $LaTeX: 2 \hat {\alpha}_{m}$ .
Sul diagramma è possibile anche determinare le componenti normale e tangenziale del vettore:

$LaTeX: s_{mn} = C + r \cos {\left( 2 \hat {\alpha}_m \right) }$ ,

$LaTeX: s_{mt} = r \sin {\left(2 \hat {\alpha}_m \right) }$ .

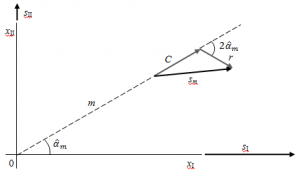
Per rappresentare il vettore $LaTeX: \bar {\mathbf{s}}_m$ nel piano x_I0x_II si procede nel seguente modo:

si traccia la direzione m inclianta di $LaTeX: \hat {\alpha}_{m}$ rispetto alla direzione x_I;
si traccia sulla direzione m la componente sferica C, uscente dalla direzione (cioè che si allontana rispetto all'origine) se C > 0, e entrante (e quindi che punta verso l'origine) in caso contrario;
si traccia la componente deviatorica r inclinata di $LaTeX: 2 \hat {\alpha}_{m}$ rispetto a m in senso opposto rispetto a quanto riportato sul cerchio di Mohr (e cioè orario se l'angolo sul cerchio di mohr è antiorario, e antiorario altrimenti).

Riportate le componenti, il vettore è immediatamente rappresentabile in quanto somma dei due vettori.

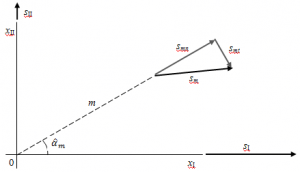
Un'altra possibilità per rappresentare il vettore consiste nell'utilizzare le sue componenti normale e tangenziale. Si procede quindi come segue:

si traccia la direzione m inclianta di $LaTeX: \hat {\alpha}_{m}$ rispetto alla direzione x_I;
si traccia sulla direzione m la componente normale s_mn, uscente dalla direzione (cioè che si allontana rispetto all'origine) se s_mn > 0, e entrante (e quindi che punta verso l'origine) in caso contrario;
si traccia la componente tangenziale s_mt perpendicolarmente rispetto a m; se sul diagramma di Mohr s_mt >0, allora sul piano x_I0x_II deve essere riportata in modo da ruotare intorno all'origine degli assi in senso orario, e in senso antiorario in caso contrario.

In particolare le regole di cui ai punti 2 e 3 della precedente lista prendono il nome di convenzione di Mohr, e permettono di tracciare in modo corretto il vettore $LaTeX: \bar {\mathbf{s}}_m$ partendo dalle sue componenti normale e tangenziale.
La convenzione di Mohr è fondamentale per eseguire la costruzione del cerchio a partire da un tensore simmetrico piano espresso nelle sue generiche coordinate:

$LaTeX: \mathbf{S} = \begin{bmatrix} s_{11} & s_{12} \\ s_{21} & s_{22} \end{bmatrix}$ ,

e per determinarne il polo.

Voci correlate

Cerchio di Mohr

Note

↑ Per fare ciò si deve immaginare anche di aver preventivamente traslato le componenti C nell'origine degli assi, e di aver di conseguenza spostato anche le parti deviatoriche r in modo da restare applicate agli estremi di C.

La consultazione di TecnoLogica è preordinata alla lettura delle avvertenze

[0] Per fare ciò si deve immaginare anche di aver preventivamente traslato le componenti C nell'origine degli assi, e di aver di conseguenza spostato anche le parti deviatoriche r in modo da restare applicate agli estremi di C.

[1]

Cerchio di Mohr/Dimostrazione

Da TecnoLogica.

Descrizione

Voci correlate

Note

Visite

Strumenti personali

Navigazione

Ricerca

Strumenti