Cerchio di Mohr

Da TecnoLogica.

Indice 1 Descrizione 2 Costruzione 3 Polo e antipolo 4 Componenti del vettore associato ad una direzione 5 Autovalori e autovettori 6 Voci correlate

Descrizione

È una costruzione geometrica che si costruisce partendo da un tensore di secondo ordine piano simmetrico grazie alla quale è possibile determinare per via grafica:

• le componenti del vettore che il tensore associa ad una generica direzione α_n;
• le direzioni principali del tensore, e i relativi autovalori.

Per fare ciò, occorre:

1. eseguire la costruzione del cerchio
2. individuare un punto notevole, detto polo.

Grazie al cerchio di mohr, i risultati grafici possono permettere anche la soluzione analitica dei problemi affrontati, tanto da essere spesso il metodo preferito rispetto alle tradizionali tecniche di determinazione tipiche dell'algebra tensoriale.
I motivi che stanno alla base dell'efficacia di questa particolare costruzione geometrica sono contenuti nel lemma che ne riporta la dimostrazione.

Costruzione

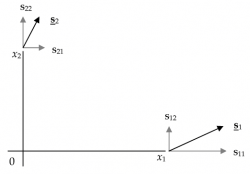
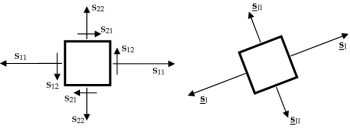
Sia dato il tensore simmetrico piano di coordinate:

,

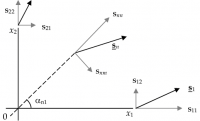
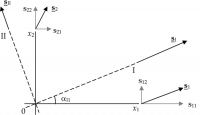
la cui rappresentazione nel piano è riportata nel disegno a fianco.
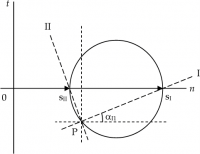
Questo tensore dà origine ad un cerchio di Mohr, che può essere tracciato seguendo le indicazioni che seguono.
Si tracci un sistema di assi coordinati ortogonali n0t, con n asse orizzontale, e si riportino su di esso i valori delle componenti s₁₁ e s₂₂; se le componenti sono positive, allora saranno positive anche le loro rappresentazioni su n.
Ad esempio, se s₁₁ = 5 e s₂₂ = 2, i punti da inserire nel diagramma per costruire il cerchio di Mohr avranno rispettivamente coordinate (5, 0) e (2, 0). Allo stesso modo, se s₁₁ = -3 e s₂₂ = 1, allora i punti avranno coordinate (-3, 0) e (1, 0).
Si procede quindi a riportare i valori delle componenti miste s₁₂ e s₂₁ secondo la convenzione di Mohr. Se nella rappresentazione del tensore (disegno in alto) la componente s₁₂ ruota in senso antiorario intorno all'origine degli assi, allora deve essere riportata negativamente sul diagramma; in caso contrario, se s₁₂ ruota in senso orario intorno all'origine, allora è positiva. Stabilito il segno, il vettore deve essere disegnato verticalmente (parallelo quindi all'asse t) a partire dall'estremo del vettore s₁₁ precedentemente tracciato sull'asse n.
Il vettore s₂₁ deve invece essere disegnato in verticale, a partire dall'estremo del vettore s₂₂, ma dal lato opposto rispetto a s₁₂. Tenendo conto quindi della convenzione di Mohr sui segni, i punti estremi dei vettori s₂₁ e s₂₂ avranno coordinate (s₁₁, -s₁₂) e (s₂₂, s₂₁); unendo questi due punti è possibile trovare geometricamente il centro C del cerchio - intersezione del segmento con l'asse n - e il raggio - metà del medesimo segmento.
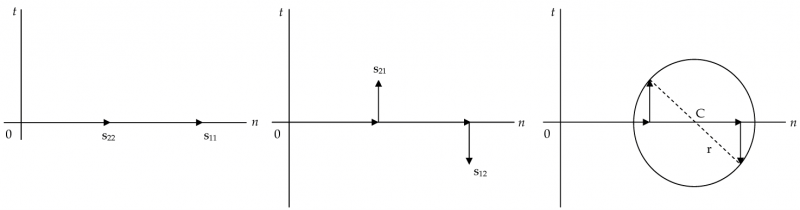
In termini algebrici, l'ascissa del cerhio è pari a:

,

mentre il raggio è:

.

Polo e antipolo

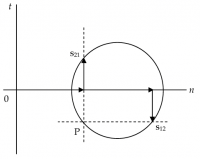
Il polo è un punto notevole che si trova sulla circonferenza; nella notazione utilizzata è contrassegnato con P.
La sua determinazione grafica è molto semplice:

1. si traccia una retta orizzontale passante per la punta del vettore che rappresenta la componente s₁₂;
2. si traccia una retta verticale passante per la punta del vettore che rappresenta la componente s₂₁;

l'intersezione tra le due rette individua il punto P.
Analiticamente, le coordinate del polo sono P = ( s₂₂, - s₁₂).
Il polo permette sia di inidividuare le componenti del vettore che il tensore associa ad una generica direzione che di trovare gli autovettori delle direzioni principali (per la procedura di entrambi, vedi i paragrafi successivi).

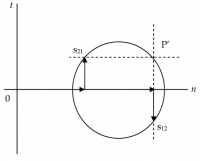
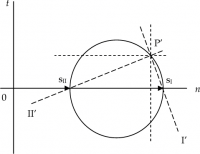
Alcune volte, però, può essere utile indivduare un secondo punto, detto antipolo, che nella notazione utilizzata è contrassegnato con P'.
L'antipolo è il punto diametralmente simmetrico rispetto al centro del cerchio; per tale motivo, volendolo determinare graficamente, si procede così:

1. si traccia una retta verticale passante per la punta del vettore che rappresenta la componente s₁₂;
2. si traccia una retta orizzontale passante per la punta del vettore che rappresenta la componente s₂₁;

l'intersezione tra le due rette individua il punto P'.
Analiticamente, le coordinate del polo sono P' = ( s₁₁, s₂₁).
L'antipolo viene utilizzato quando occorre individuare le direzioni perpendicolari rispetto alle direzioni principali, cosa che spesso occorre quando si analizzano i tensori di tensione.

Componenti del vettore associato ad una direzione

Il tensore simmetrico piano , come ogni tensore, associa ad ogni direzione del piano n, individuata dai suoi coseni direttori α_1n e α_2n, un vettore s_n secondo la legge di trasformazione dei tensori. Il cerchio di Mohr permette di costruire graficamente il vettore s_n utilizzando la procedura che segue.
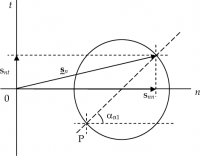
A partire dal polo P si traccia una retta inclinata rispetto all'asse orizzontale di un angolo tale che il suo coseno sia pari a α_1n. Questa retta incontra il cerchio su un punto; se si collega il punto trovato con l'origine, il vettore che si ricava è l'immagine di s_n, vettore associato alla direzione tracciata.
Scomponendo s_n sugli assi coordinati n e t, si ottengono le componenti s_nn e s_nt, grazie alle quali è possibile tracciare s_n direttamente nel sistema di assi coordinati ortogonali x₁0x₂, dove sono riportate le componenti del tensore.

Tracciata la direzione sul piano x₁0x₂, le componenti s_nn e s_nt giacciono la prima lungo la direzione stessa, e la seconda sulla perpendicolare ad essa. I versi sono stabiliti secondo la convenzione di Mohr:

• se s_nn è positiva sul piano n0t, allora s_nn è uscente dalla direzione (cioè si allontana dall'origine degli assi); in caso contrario, s_nn è entrante nella direzione (cioè si rivolge verso l'origine degli assi);
• se s_nt è positiva sul piano n0t, allora s_nt è orientata in modo da ruotare in senso orario intorno all'origine degli assi x₁0x₂; in caso contrario, allora s_nt è orientata in modo da ruotare in senso antiorario intorno all'origine degli assi x₁0x₂.

Una volta tracciati s_nn e s_nt sul sistema di assi x₁0x₂, è possibile ottenere anche il vettore s_n, che è la somma vettoriale delle due componenti.

Si noti che s_n sul piano n0t e s_n sul piano x₁0x₂ sono orientati diversamente: il cerchio di Mohr infatti non dà alcuna informazione sull'incilinazione del vettore, ma solo sul valore delle sue componenti.

Autovalori e autovettori

Per definizione, gli autovalori di un tensore simmetrico sono i moduli di quei vettori che hanno la proprietà di essere collineari alle direzioni ad essi associate dal tensore stesso.
Secondo la costruzione di Mohr, questa proprietà si verifica per quei vettori individuati dal cerchio che non hanno componente sull'asse t. Questa caratteristica si riscontra solo in due punti, e cioè nelle intersezioni del cerchio con l'asse n.

Conosciuti quindi centro e raggio del cerchio, gli autovalori s_I e s_II sono immediatamente determinati grazie alle relazioni:

e .

Nota la posizione del polo P, gli autovettori delle due direzioni principali sono immediatamente determinati congiungendo il polo con i vertici dei vettori s_I e s_II.
Analiticamente è sufficiente determinare solo uno dei quattro coseni direttori che individuano le direzioni principali I e II, perché le direzioni sono mutuamente ortogonali, ed è quindi semplice calcolare i restanti tre valori partendo dal primo.
Scelto ad esempio l'angolo , la sua tangente è pari a:

Conosciuta la tangente dell'angolo, è poi possibile calcolarne il valore (estraendo l'arcotangente) e quindi il coseno direttore (calcolandone appunto il coseno). Per conoscere gli altri angoli, sussistono le relazioni:

Quando occorre determinare le direzioni perpendicolari rispetto a quelle principali, invece di utilizzare il polo P del cerchio si impiega l'antipolo P'. La procedura è la medesima: dal punto P' si conducono due rette passanti per i vertici dei vettori s_I e s_II; in questo caso, le relazioni che legano le direzioni principali I e II alle omologhe antipolari I' e II' sono le seguenti:

Per inciso, la ricerca delle direzioni antipolari è particolarmente utile quando il tensore è rappresentativo di una caratteristica di un corpo piano (vedi figura sopra): queste infatti permettono di determinare immediatamente la giacitura delle facce di un elemento infinitesimo di materia sulle quali agiscono gli autovalori del tensore.

Voci correlate

• Autovalore
• Autovettore
• Dimostrazione
• Direzione principale
• Tensore piano
• Tensore simmetrico

La consultazione di TecnoLogica è preordinata alla lettura delle avvertenze Ogni contributore è responsabile dei propri inserimenti. Il progetto è opera di Luca Buoninconti © 2011-2024.