Attenuazione acustica
Da TecnoLogica.
Indice |
Descrizione
Le attenuazioni acustiche sono quelle aliquote che occorre sottrarre al livello di pressione sonora per ottenere l'intensità del suono o del rumore che si può udire in un punto prefissato di ascolto.
Detto cioè il livello di potenza sonora della sorgente, il livello ascoltato in un determinato punto è pari a[1]:
dove è l'attenuazione, e
un coefficiente di correzione della direzionalità.
L'attenuazione in realtà è la somma di diverse aliquote, dovute:
- alla divergenza geometrica;
- all'assorbimento atmosferico;
- all'effetto suolo;
- alla presenza di barriere;
- alla presenza di vegetazione;
- alla presenza di costruzioni industriali;
- alla presenza di costruzioni urbane.
Il coefficiente di correzione della direzionalità tiene conto dell'incremento di pressione sonora che si verifica quando il suono o il rumore viene emesso in una direzione specifica, allontanandosi cioè dal modello di sorgente puntiforme omidirezionale. In tal caso, il coefficiente è somma di due aliquote:
, che tiene conto della direzionalità;
, che tiene conto della riduzione dell'angolo solido di propagazione.
Quando è noto il livello di pressione sonora ad una distanza nota e se ne vuole calcolare il livello ad una diversa distanza
, la relazione:
,
permette di eseguire il calcolo quando sia presente esclusivamente la divergenza geometrica.
Divergenza geometrica
La divergenza geometrica tiene conto del decremento del segnale sonoro dovuto alla distanza tra l'ascoltatore e la sorgente.
Se la sorgente può considerarsi puntiforme e omnidirezionale, allora il segnale si propagherà diffondendosi sfericamente intorno al punto di origine. In tal caso l'attenuazione, in decibel, risulta pari a[1]:
,
dove d è la distanza tra la sorgente e l'ascoltatore, espressa in metri.
Nel caso in cui la sorgente si considera lineare, di lunghezza infinita, il suo decadimento si calcola come:
.
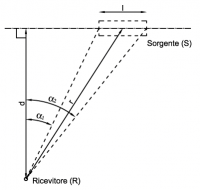
Se la sorgente è lineare, ma di lunghezza finita , l'attenuazione deve essere invece calcolata con al seguente relazione:
,
dove è la distanza minima (in metri) tra il ricevitore e l'asse della sorgente,
è la distanza (in metri) tra il ricevitore e il centro della sorgente, mentre
e
sono gli angoli di vista (in radianti) entro i quali il ricevitore vede la sorgente lineare.
Assorbimento atmosferico
La diffusione del suono può essere ridotta dall'atmosfera in funzione della temperatura dell'aria, dell'umidità e della frequenza del segnale.
La relazione che permette di calcolare l'attenuazione è[1]:
dove è la distanza tra la sorgente e il ricevitore (in metri), e
è un valore tabellato in funzione della temperatura e dell'umidità. Per i casi più comuni è possibile utilizzare i seguenti valori:
| Temp. [°C] | Um. rel. [%] | Coefficiente di attenuazione atmosferica α [dB/km] | |||||||
|---|---|---|---|---|---|---|---|---|---|
| Frequenza nominale [Hz] | |||||||||
| 63 | 125 | 250 | 500 | 1000 | 2000 | 4000 | 8000 | ||
| 10 | 70 | 0.1 | 0.4 | 1.0 | 109 | 3.7 | 9.7 | 32.8 | 117 |
| 20 | 70 | 0.1 | 0.3 | 1.1 | 2.8 | 5.0 | 9.0 | 22.9 | 76.6 |
| 30 | 70 | 0.1 | 0.3 | 1.0 | 3.1 | 7.4 | 12.7 | 23.1 | 59.3 |
| 15 | 20 | 0.3 | 0.6 | 1.2 | 2.7 | 8.2 | 28.2 | 88.8 | 202 |
| 15 | 50 | 0.l | 0.5 | 1.2 | 2.2 | 4.2 | 10.8 | 36.2 | 129 |
| 15 | 80 | 0.1 | 0.3 | 1.1 | 2.4 | 4.l | 8.3 | 23.7 | 82.8 |
Per i valori intermedi si può interpolare linearmente. Per intervalli di temperatura e di umidità non compresi nella tabella, o per ottenere risultati più precisi, è possibile utilizzare questa pagina per eseguire il calcolo secondo le indicazioni della norma ISO 9631-1:1993.
Effetto suolo
Questa attenuazione si verifica esclusivamente quanto il segnale attraversa una zona il cui suolo è poroso o misto, con predominante porosa, per cui il suono viene parzialmente assorbito dalla superficie. In pratica, questa attenuazione deve essere aggiunta alle altre quando il suolo tra la sorgente e il ricevitore è di tipo terroso: suoli rocciosi o pavimentazioni artificiali non hanno capacità assorbente, ma anzi riflettono le onde intensificandone la percezione da parte dell'ascoltatore. Inoltre, il segnale non deve essere un tono puro.
In tal caso, l'attenuazione cercata è pari a[1]:
,
dove:
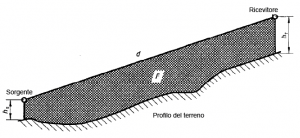
è la distanza in linea d'aria (in metri) tra ricevitore e sorgente;
è l'altezza media alla quale si trova la congiungente sorgente-ricevitore ed il suolo; con riferimento alla figura a lato, se
è l'area sottesa da detta congiungente,
.
Se la relazione sopra riportata genera valori negativi, deve essere considerata nulla.
A causa della parziale riflessione dell'onda sonora sul terreno, occorre introdurre un coefficiente di direzionalità pari a:
dove e
sono le altezze di sorgente e ricevitore (in metri) rispetto al terreno, e
è la proiezione della distanza
(in metri) sul piano orizzontale.
Barriere
(da compilare)
Vegetazione
La vegetazione fitta, composta cioè da piante ed alberi molto ravvicinati, è in grado di ridurre l'intensità del segnale sonoro, perché parte dell'energia associata all'onda acustica viene trasferita al fogliame.
Nell'eseguire la valutazione, occorre considerare che la linea di propagazione del segnale, a causa della rifrazione atmosferica, segue una traiettoria curva del raggio approssimativo di 5 km. Tracciata in sezione questa curva, conoscendo anche l'altezza degli alberi, è possibile calcolare le lunghezze d1 e d2 corrispondenti alla porzione di curva che attraversa la vegetazione. In alternativa, la curva può essere sostituita da due tratti rettilinei inclinati di 15° rispetto al piano orizzontale. Espresse le distanze in metri, se ne calcola la somma df=d1+d2.
Nel caso df<10 m, l'attenuazione è nulla. Se df è compresa tra 10 e 20 metri, allora l'attenuazione è pari a[1]:
| Distanza [m] | Frequenza nominale [Hz] | |||||||
|---|---|---|---|---|---|---|---|---|
| 63 | 125 | 250 | 500 | 1000 | 2000 | 4000 | 8000 | |
| 10m ≤ df ≤ 20m | 0 dB | 0 dB | 1 dB | 1 dB | 1 dB | 1 dB | 2 dB | 2 dB |
Quando invece df è maggiore di 20 metri, ma minore di 200, l'attenuazione è pari a:
,
dove il coefficiente si ricava dalla seguente tabella:
| Distanza [m] | Frequenza nominale [Hz] | |||||||
|---|---|---|---|---|---|---|---|---|
| 63 | 125 | 250 | 500 | 1000 | 2000 | 4000 | 8000 | |
| 20 ≤ df ≤ 200 | 0.02 dB/m | 0.03 dB/m | 0.04 dB/m | 0.05 dB/m | 0.06 dB/m | 0.08 dB/m | 0.09 dB/m | 0.12 dB/m |
Per valori superiori, si applica comunque l'attenuazione che si avrebbe se df fosse pari a 200m.
In ogni caso dovrà comunque essere che ≤ 10 dB.
Costruzioni industriali
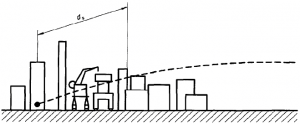
Se il segnale sonoro supera una località in cui sono presenti costruzioni di tipo industriale, la sua intensità diminuisce con la seguente legge[1]:
,
dove è la distanza (in metri) che il suono percorre attraverso le costruzioni seguendo una traiettoria curva o inclinata come descritto nel precedente paragrafo, e
è un coefficiente che può essere ricavato dalla seguente tabella:
| S [dB/m] | Frequenza nominale [Hz] | |||||||
|---|---|---|---|---|---|---|---|---|
| 63 | 125 | 250 | 500 | 1000 | 2000 | 4000 | 8000 | |
| 0.0 | 0.015 | 0.025 | 0.025 | 0.02 | 0.02 | 0.015 | 0.015 | |
In ogni caso, non può essere superiore a 10 dB.
Costruzioni urbane
Se il segnale sonoro supera una località in cui sono presenti costruzioni di tipo urbano, l'assorbimento che subisce è pari a[1]:
;
;
.
La prima aliquota si applica sempre; la distanza
(in metri) è concettualmente analoga alla distanza
dovuta alla vegetazione, mentre
è la densità edilizia, espressa come rapporto tra la superficie occupata dagli edifici rispetto alla superficie totale.
La seconda aliquota si applica soltanto nei casi in cui la sorgente è di tipo lineare, come una strada o una linea ferroviaria, ed ai lati sorgono delle costruzioni. In tal caso, il valore
è espresso come rappoto tra la lunghezza occupata dalle facciate degli edifici diviso la lunghezza totale dell'infrastruttura, in percentuale. Questo valore deve comunque essere minore o uguale a 90%.
Conoscito quindi il valore di , ed avendo già calcolato quello di
:
- se
≥
, nel calcolo finale si terrà conto solo di
, come se
= 0;
- se
<
, nel calcolo finale si terrà conto solo di
, come se
= 0.
Note
|